Zrakové zážitky tvaruje perspektiva. Souhra lidských smyslových vjemů vede k názoru, že jejich příčinou je hmota. Ta má být jednoduše rozmístěná v lineárním Euklidově prostoru. Jenže matematizace takového prostoru často nedává výsledek. Počítá nekončící iracionality, například Ludolfovo číslo π. Sebevědomě popisujeme Vesmír zaokrouhlováním neznámých výsledků. Neexistujících výsledků.

    Naopak jednoduše pojatý prostor perspektivního vidění lze matematizovat vždy racionálně. Poskytne konečný výsledek. Navíc do perspektivního prostoru lze přecházet z diskrétního (bodového). Euklidův prostor se vynechá.

    Matematika stanovila poměr zlatého řezu 1:1,618... Užitím iracionálního - neskutečného čísla.

    Řešení v jiné geometrii, v perspektivním prostoru, vyčísluje ten samý zlatý řez jiným poměrem.

1. Úvod

Zlatý řez vyjadřuje mimořádný poměr dvou stran obdélníka. Vyznačuje se ladností, pro kterou lidé vybírají tento poměr stran - když dbají svého dobrého pocitu. Zlatý řez má mít uplatnění nejen ve výtvarném umění, fotografii a architektuře, ale i v hudbě, v biologii i v posuzování rozměrů lidského těla.

Matematika zdůvodňuje, co je poměrem zlatého řezu.

Obr. 1. Obdélník zlatého řezu. Poměr jeho stran v geometrii a v matematice

««« SLEDOVAT VŠECHNY OBRÁZKY I V LEVÉM SLOUPCI

Obrázek se zlatým řezem ukazuje dva podobné trojúhelníky (obr. 1). Menší má odvěsny: b a a, větší: a a (a+b). Znázorňují poměry vyjádřené rovnicí.

Vztah dvou stran obdélníka zlatého řezu je následovný. Poměr součtu obou stran a + b ku delší straně a je roven poměru delší strany a ku kratší b. Vypočítaný poměr je a/b = (1 + odmocnina z 5)/2.
Podíl vychází iracionální:

Gustav Theodor Fechner ověřoval jev zlatého řezu hodnocením lidských pocitů a názorů a potvrdil ho [1].

Ještě i ve 20. století byl jev znovu posuzovaný - odmítaný nebo přijímaný. Upřednostňování obdélníka s takovým poměrem stran je staré tisíce let, proto tento přístup nepodcením.

2. Euklidův prostor

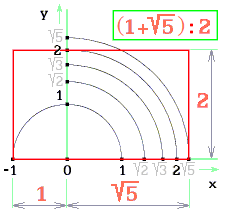
Obdélník sestrojím v poměru stran (1 + √5)/2 a to v Euklidově prostoru (obr. 2). Svislou stranu obdélníka zvolím b = 2, a delší vodorovnou stranu a = 1 + √5 = |-1| + √5.

Pro grafické zobrazení výrazu vyznačím 1 do záporného směru. Poměr zlatého řezu je daný iracionálním číslem, jak určuje odmocnina z 5. Tedy nepřesně.

Obr. 2. Zlatý řez v Euklidově prostoru

3. Perspektivní prostor

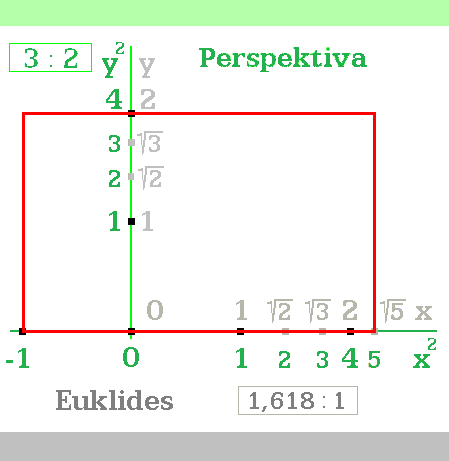
Dál poměr prověřím v perspektivním prostoru. Perspektiva má jinou geometrii, proto i matematický poměr bude jiný. Jestliže výraz (1 + √5)/2 není ničím vyjímečný, zde se to může změnit. Přepočet stran obdélníka b = 2, a = 1 + √5  je snadný; výraz určuje, do kterého místa obrazec zakreslit. Souřadnice bodů [-1;0], [√5;0], [0;2] umocním na druhou. Nové souřadnice [-(-1)²;0], [5;0], [0;4] rozmístím v perspektivním prostoru (obr. 3).

Obr. 3. Zlatý řez v perspektivním prostoru

• Jednotková délka se převádí beze změny - na vodorovné ose do úseku od 0 k záporné jedničce.
  
• Délku √5 nahradí délka 5.
  
• Svislou délku b = 2 nahradí délka 4.

Perspektiva: Matematika vyjádřila délky stran bez zaokrouhlení - přesně. Na obrázku vznikl obdélník o stranách b = 4 a a = 6. Příčinou odlišného údaje o délkách je jiný průběh cejchování os.

4. Racionální obdélník

Z diskrétního do perspektivního prostoru se body převádějí přesně. Přitom dodrží kartézské souřadnice a vzdálenost od počátku. Nevypočítatelné iracionality se nevyskytnou. Pak naše perspektivní zážitky posuzuji, že jsou odvozené z diskrétního prostoru (obr. 4). Ten ať je zásobárnou údajů pro smyslové vjemy tvora (obr. 5). Perspektivní prostor užívá osy cejchované kvadratickým měřítkem. V odvěkém zrakovém prostoru je poměr stran již nikoliv  1:1,618..., vždy nepřesných, nýbrž 2:3.

5. Zlatý řez proměnlivě vnímaný

Obr. 6. Vjem pozorovatele A a B mění perspektiva

5.1. Obdélník těsně u očí

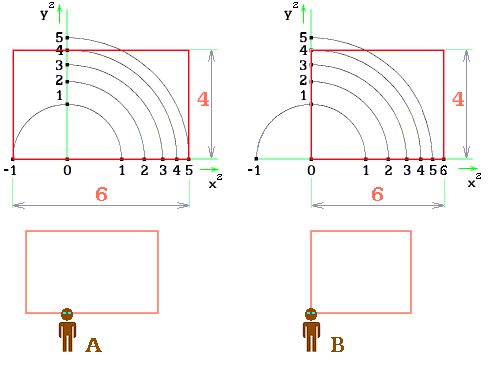
Vjem v postavení A odpovídá odvození iracionálního výrazu (1 + √5)/2 Euklidova prostoru. Kdežto je-li pozorovatel B umístěný ve vrcholu obdélníka, pak mu perspektiva zkrátí delší stranu výrazněji než tomu v postavení A. To proto, že délku 0-1 vnímáme větší než délku 5-6.

5.2. Obdélník pozorovateli vzdálený

Obraz visí na stěně a má strany poměru zlatého řezu, zde 1,62 × 1 metr (obr. 7). Pozorovatel je od jeho středu vzdálený 4 metry. Jak moc se uplatní perspektivní zkreslení na vjem dvou stran obrazu?

V Euklidově prostoru počítám Pythagorovou větou, jaké jsou tři různé vzdálenosti pozorovatele od tří bodů na obraze. Vychází, že pozorovatelovy vzdálenosti od středu obrazu, od vrchu a zprava se liší jen málo: 4 metry, 4,03 m a 4,08 m.

Pozorovatel vnímá zlatý řez, protože všechny čtyři strany obdélníka jsou od něj vzdálené skoro stejně. Nepatrné zkreslení perspektivou nevnímá.

Vjem zlatého řezu souvisí s pozorovatelovou vzdáleností od objektu. Ve větší vzdálenosti není vjem zkreslený.

Obr. 7. Pozorovatel je hodně vzdálený od obrazu

6. Zobecnění

Vjem obdélníka zlatého řezu je podmíněný místem, odkud objekt pozorujeme. Můžeme jej vidět v poměru stran 2:3, hodnoceno perspektivní geometrií.

Neposoudím, které různé vlivy nás k oblibě zlatého řezu vedou. Zda jsou obsažené v našem vědomí či v konstrukci Vesmíru, což může být totožnou záležitostí. Jedna zajímavost se však nabízí.

Je to jeden z obdélníků, jejichž poměry délek stran jsou určeny nejmenšími přirozenými čísly. Sestavení obdélníka 2:3 spotřebuje 2+2+3+3 = 10 jednotkových délek. Nejmenší obdélník by měl strany v poměru délek 1:2, sousední nejúspornější by byl 1:3, další úsporný je potom jak 1:4, tak i obdélník zlatého řezu 2:3. Není to tedy žádný lhostejný poměr například 214:383. Avšak většinou, v současnosti, nedbáme promyšlené konstrukce Vesmíru. Svět se měl vytvořit, i se svým zlatým řezem, zcela bez návrhu, lhostejně? Sám od sebe?

Rovněž kmitočty tónů libozvučných hudebních akordů jsou dány poměrem právě malých celých čísel.

7. Závěr

Jestliže ten samý jev můžeme hodnotit těmito dvěma způsoby, pak který z užitých prostorů lépe vystihuje skutečnost našeho světa? Ačkoliv Euklidův prostor je vhodný pro obvyklá výpočetní využití, naopak diskrétní prostor nepoužívá zaokrouhlení; zdárněji popisuje náš svět. Umožňuje absolutně přesné výpočty.

Naopak prostor, jenž pro některé geometrické vlastnosti našeho Vesmíru nemá řešení, vesmírnou geometrii nevystihuje. Což posuzuji jako axiom: konečné velikosti fyzikálních veličin vyjadřují racionální čísla. Pokud to není splněno, pak vybraný geometrický prostor není obrazem našeho světa.

Výběrem, mezi matematikou Euklidova a perspektivního prostoru, lze posoudit, zda základem fyziky Vesmíru je lidské vnímání nebo lineárně rozložená hmota. Skrývá se za perspektivním viděním Euklidův anebo bodový prostor? Je-li základem světa právě lidské vnímání, pak svět je promyšleně vytvořenou realitou.

[1] Mario Livio: Zlatý řez. Nakladatelství Dokořán, Praha 2006.