Čtyřrozměrná koule geometricky
💾

Bohumír Tichánek
* * *

Po začátku 20. století Einstein zjistil, že zavedený pojem éteru nemá opodstatnění. Odmítnout takovou náplň volného prostoru, to byla zásadní změna. Samotný pojem prostoru byl znejistěn. Jsou jen vzdálenosti mezi kusy hmoty a prostor nemá žádné vlastnosti?
Nyní se uplatňuje na sestavu světového prostoru víc názorů. Časoprostor může být spojitý nebo nespojitý. Geometrická konstrukce objektů 4D (čtyřrozměrného) prostoru nasvědčuje nespojitosti - sestavě z jednotlivých sousedících 3D objemů. Pak i náš 3D prostor se nabízí jako bodový; lépe než spojitý podle Eukleida nebo převažujících teorií.
Čtverec bodového prostoru, přepočtený do prostoru zrakové perspektivy, vytvoří kružnici.
Analogicky z krychle vznikne koule. Nebo z 4D krychle - 4D koule. Vzniklý n-rozměrný útvar bude nespojitý. Složený z navršených (n-1)-rozměrných útvarů rozdílných velikostí, rovněž tvořených body. Například koule vznikne z kruhů.
OBSAH
Obr. 1. 4D krychle vzniká spojením všech rohů krychle s další krychlí
««« SLEDOVAT VŠECHNY OBRÁZKY I V LEVÉM SLOUPCI
Matematika skládá 4D prostor ze 3D prostorů. Jejich počet posuzuje jako nekonečný. Tento názor je zdůrazněný smyslovým poznáním hmoty.
Zavedu-li bodový prostor namísto spojitého, pak do konstrukce 4D prostoru vložím konečný počet použitých objemů. Takový popis
stavby prostoru je úměrný našim technickým postupům. Málo mu odpovídá prostor, tvořený body nekonečně blízkými, v prostoru rozloženém do nekonečna.
Z bodového prostoru lze body přepočítávat do perspektivního zobrazení [1]. Zachovají si přitom svou vzdálenost od počátku a své kartézské souřadnice. Kdežto přepočet z prostoru bodového do Euklidova není možný. Postup [1] zdůrazňuje důležitost smyslového vnímání - zraku a sluchu.
Bodový prostor přiblíží konstrukci čtyřrozměrné krychle. Tvoří ji tolik oddělených objemů, tolik krychlí, kolik bodů čítá délka hrany (obr. 2). Důvěryhodnost bodového prostoru podporuje Planckova délka.
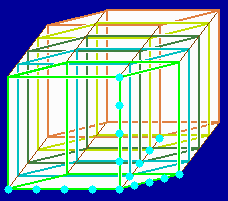
Obr. 2. 4D krychli tvoří sousedící krychle, jež se jakoby prostupují, posunuté o 1 posici
Plošný 2D tvor, Stín, vládne 1D zrakem (obr. 3). Neuvidí kružnici; namísto oblouku uvidí jen úsečku. Pokud je vybavený dvěma očima, podle vzoru člověka, pak vidí plošně. Vnímá hloubku - druhý rozměr svého 2D světa, takže namísto úsečky tuší oblouk.
Nevidí do hloubky Zeměkruhu, na kterém žije. Takový pohled je přístupný až z vyššího 3D světa.
Obr. 3. Vidění ve 2D světě
Kružnice vznikne převodem čtverce z diskrétního do perspektivního prostoru. Viz body ABCDEF v obrázku.
Představím nejmenší kouli bodového prostoru. Její povrch tvoří 6 zelených bodů, zahrnutých v jediném 3D objemu 4D bodového prostoru
(obr. 5).
Obr. 5. Diskrétní kouli ve 4D prostoru tvoří šest zelených bodů kolem středu
V objemu bodového prostoru má bod šest jiných bodů sousedních. V 4D prostoru jich má osm. Kterýkoliv z osmi povrchových bodů je od
středu vzdálený jeden krok. Povrch nejmenší 4D koule bodového prostoru tvoří osm bodů (obr. 5).
Kouli v zásadě vidíme ve tvaru pouhého kruhu, neboť sítnice oka je jen dvojrozměrná.
Stín, obyvatel plošného světa, se pokouší zobrazit kouli nadřazeného 3D prostoru. Správně zobrazil obrys koule - kruh, ale nezohlednil směr pohledu (obr. 6). Kružnice, jimiž je povrch koule tvořen, měl přetvarovat v elipsy (obr. 6.a). Stín však nezná takové zkreslení svých kružnic. Vídá z nich jen úsečku - půlku obvodu kružnice.
Při pozorování koule nevidíme obsah žádné z povrchových kružnic; vnímáme jen jejich obvody. Tvoří-li kouli miliarda rovnoběžných kruhů, nabízí se naráz půl miliardy kružnic. Vidíme polokouli (obr. 7).
Jsou snad soustředné i ve skutečnosti, nejen na použitém obrázku? Nejsou. Jen zdánlivě se řadí, promítáním z 3. směru 3D prostoru na plochu, jako soustředné kružnice. Ve skutečnosti jsou umístěné v různých místech, vzájemně nad sebou, na nezobrazené ose „z“ 3D prostoru.
Obr. 8. Polokouli tvoří 11 útvarů: 9 půlkružnic, jež se zobrazují jako úsečky, a 2 body. Třetí osu „z“ zobrazuje bod počátku 0
Jenže - obrazem kružnice v bodovém prostoru je čtverec, postavený na svém vrcholu (obr. 9).
Podobně pro 4D prostor zpřesním sestavu diskrétní 4D koule. Všechny body jejího povrchu jsou - od středu největšího tělesa - vzdálené stejný počet kroků (obr. 10).
Podle způsobu 6.1. (ve 3D prostoru) odvozuji postup 6.2. (ve 4D prostoru).
Kruh mu vytvářely jedním či druhým způsobem:
6.1.1. - ty kružnice, jež ukazovaly polokouli, pozorovateli přivrácenou (obr. 7). Zda je koule dutá nebo ne, se nepozná.6.1.2. - ty úsečky (půlkružnice), jež ukazovaly polokouli, pozorovateli přivrácenou (obr. 8). Zda je koule dutá nebo ne, se nepozná.
Podobně - Člověk pozoruje 3D kouli jen jako kruh - vždyť máme 2D vidění.
Když čtyřrozměrný člověk (Čtverák) pozoruje 4D kouli, nevidí sled objemů, sled koulí. Vidí jedinou kouli - svým 4D zrakem vnímá všechny její vnitřní body.
Jako i my, pokud by koule byla sestavená z kruhů (od nejmenšího k největšímu a dál naopak), pak člověk by viděl kružnice. Ty by mu skládaly kouli.
Dle postupu 6.2.1.:
6.2.1. - Objem největší koule vytvoří ty povrchy menších koulí, jež skládají jemu přivrácenou 4D polokouli. Podílely se koule 1, 2, 3, 4 (obr. 11). To proto, že Čtverák vidí objem za objemem; jenže následná vzdálenější koule je mu skoro celá skrytá tou bližší. Vidí vždy jen povrch vzdálenější koule, protože ten přesahuje onu bližší kouli.Čtverák nepozná, zda je 4D koule dutá nebo ne. Zda jsou jednotlivé koule duté nebo ne.
Obr. 12. 4D koule, sestavená z koulí. Pohled ve 4. směru 4D prostoru - nedokonale je zobrazeno 6 útvarů 4D polokoule. Proč nedokonale?
Obr. 13. Polokoule vyznačená elipsami
Čtyřrozměrná koule sestává ze sledu zmenšovaných koulí, promítáním zdeformovaných. Tomu nasvědčuje povrch 4D krychle - vždyť i ten, v promítnutí na plochu, ukazuje podivně zdrcené povrchové krychle. Obdobný účinek zde deformuje koule v elipsoidy.
Čtverák vidí celou malou fialovou kouli – vnímá veškerý její objem, zakrytý jen černým bodem. Ostatní deformované koule se částečně zakrývají; nevnímá všechny body jejich objemu. Vidí celé jejich povrchy, což 2D obrázek nevystihne.
Na dalším obrázku (obr. 15.a) sledujme nejprve jeho spodní část. Sestavou ať je povrch koule, rozložený v sedm útvarů. Útvarem 2. až 6. jsou kružnice, jež tvoří povrch koule. Červený bod obíhá po hlavní kružnici rozebrané koule.
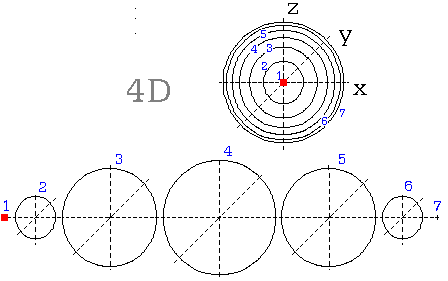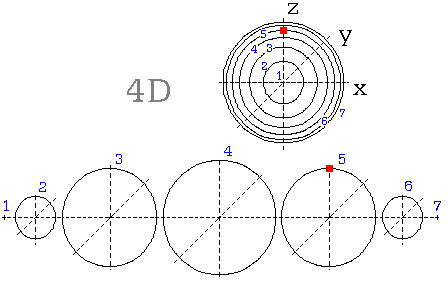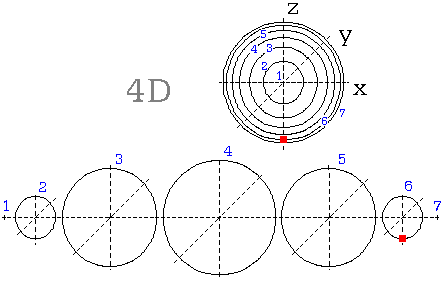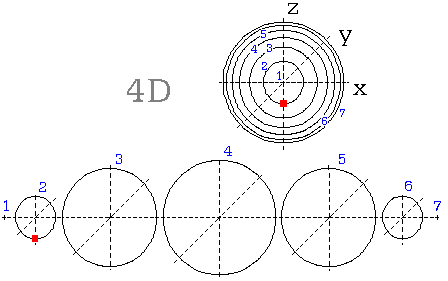
Co však zobrazuje horní část (obr. 15.b), jak vlastně souvisí s dolním obrázkem?
Bernhard Riemann v 19. století zdůvodňoval náš Vesmír jako hmotu, jež je rozložená na povrchu 4D koule. V dalším chápejme dolní obrázek odlišně; je to 4D koule, rozložená na jednotlivné koule, v sousedních objemech 4D prostoru.
Horní obrázek pak zobrazí vjemy pozorovatele, jenž je umístěný nalevo, v bodové posici 1. objemu. Když se mu vzdaluje objekt do Vesmíru, předpokládá jeho vzdalování po přímce. Netuší, že žije na povrchu 4D koule a že tedy jeho prostor je z hlediska 4D prostoru zakřivený. Zakřivení svého 3D prostoru sice nepozorujeme, jenže - tak jako je zakřivený povrch koule, je nutně zakřivený i povrch 4D koule. (Zde prosím nesměšovat se zakřivením časoprostoru).
Jeho vjem je mu daný horním obrázkem. Vždyť i my: svůj svět můžeme chápat jako soubor rostoucích koulí, v jehož středu se nacházíme.
Světelný paprsek sleduje zakřivenou trasu, a žádné síly k tomu na něj nemusí působit. Trasa je přepočtená z posic diskrétního prostoru.Podivný jev nastane, když bod dospěje do nejvzdálenějšího 7. objektu, do nejvzdálenějšího místa, jež také tvoří 4D kouli. Světelné paprsky nyní přicházejí pozorovateli, do 1. objektu, současně ze všech stran.
Pak se bod vrací k pozorovateli, v obou obrázcích, spodem.
Model ukazuje dávno známý názor, že můžeme žít v prostoru, kterým by vesmírný koráb letěl stále přímo a přece by se nakonec vrátil do místa, odkud odletěl.
Výběr průměrů užitých kružnic připomíná, že naše vnímání je perspektivní. Kružnice, jež jsou pozorovateli z 1. bodu stále vzdálenější, se na horním obrázku zvětšují stále pomaleji. Ovšem jejich rozměry, ve prospěch obou konstrukcí, nebyly vypočtené. Návrh kružnic prospívá toliko naukovému modelu.
Někdy náš Vesmír zdůvodňujeme rovnicemi, jež nedají výsledek. Užitek z kvadratické rovnice nejčastěji vznikne zaokrouhlením.
Namísto toho, vycházíme-li z bodového prostoru, lze přesné hodnoty převádět přímo do perspektivy smyslových vjemů. A kvadratické rovnice se transformují v lineární.
Užívám postupů, jež svět nabízejí jako sestrojený a námi vnímaný. Vznik promyšleně vystavěného informatického objektu nepovažuji za zázrak.
Domnívám se, že záměrná konstrukce neumožní fyzikálním veličinám, aby nabývaly velikosti nekonečně malé nebo velké.
Při hledání vycházím z technických postupů - například pro zdůvodnění časového axiomu v teorii relativity.
Děkuji zájemcům za trpělivé posuzování předložených nápadů.
* * *