V našem vidění světa mění vzdálený Měsíc svou velikost. Když se objeví na obzoru, je velký a během stoupání po obloze se brzo zmenší. Tento lidský vjem dosud nemá přijaté vysvětlení. Návrh z širšího textu IV zde krátce prohlubuji.

1. Úvod
2. Plynulé zvětšování zážitku
3. Hledání měřítka
4. Hledání výšky
   4.1. Na horách
   4.2. V nížině
5. Závěr

1. Úvod

Obr. 1. Převod bodů z diskrétního do perspektivního prostoru (kontinua) dodrží souřadnice a vzdálenost od počátku

Stoupáním Měsíce po obloze se nemění zorný úhel, který mu naměříme. Velký Měsíc je snad optický klam, daný porovnáváním objektů na obzoru – stromů a domů s Měsícem? Tento názor je někdy nabízen. Jenže zmenšovaný Měsíc bývá pozorovaný stejně tak i nad oceánem. Tento problém sleduji v souvislosti se samotnou konstrukcí lidského vnímání!

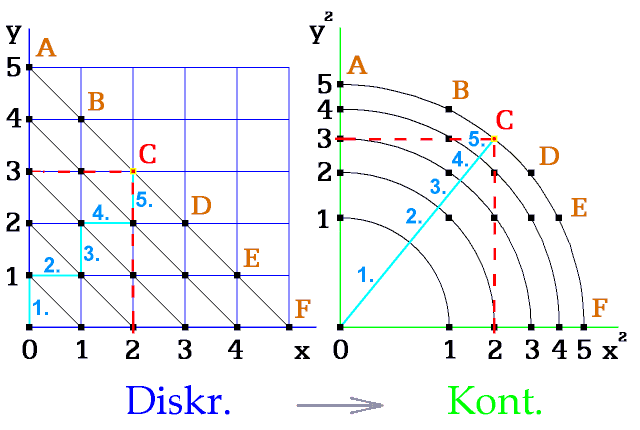
Perspektivu zakresluji po převodu bodů z bodového - diskrétního prostoru (obr. 1). Tamní čtverec, postavený na vrchol, pak v perspektivě (osy x², y²) vytvoří kružnici. Euklidův iracionální prostor neuplatňuji.

Obr. 2. Měsíc stoupá z I do II

2. Plynulé zvětšování zážitku                 

Obr. 3. Začátek zkreslování vnímané velikosti

Někdy oceňujeme impozantní dojem z velmi vzdáleného pohoří. Kopec, dosažitelný čtvrt hodinou chůze, nic zvláštního neukazuje. Ale pohled na hory, vzdálené desítky kilometrů, bývá působivý. Třeba jen na vršky Pálavy, vysoké kolem 500 metrů a vzdálené od Brna 40 km. To má menší výšku.

Měsíc nebo souhvězdí Orion, jsou-li nízko nad obzorem, jsou velmi zvětšené. Nejsnadněji lze předpokládat, že dalekým objektům, nízko nad obzorem, se s jejich dalším vzdalováním náš proměnlivý zážitek zesiluje plynule. Je tedy možné, že už i hory, vzdálené jen desítky kilometrů, dávají člověku mírně zvětšený vjem.

Jenže hory nezačnou obloukem stoupat po obloze, takže tento možný zážitek si neověříme. Vzdálená hora nestoupá na nebe a neukáže postupné zmenšování, jak činí nebeské objekty.

Nakreslené objekty ve vzdálenosti 10 km a 20 km jsou zobrazované naprosto bez zkreslení své velikosti, během svého stoupání (obr. 3). To ukazují dva šedé oblouky, vzdálené 20 km; jsou stejně velké, po 45°.

Teprve vzdálenost 30 km vytváří nestejné oblouky. Oblouky (I) zabírají asi po 35°, kdežto na třetí hnědý (II) zbývá jen 20°. Takže objekty – hory vzdálené do dvaceti kilometrů, by neměnily svou velikost, když by opisovaly kolem pozorovatele oblouk směrem nahoru. (Věřme, že takový jejich pohyb nikdo neuvidí)./p>

Toto délkové měřítko je vymyšlené, vzdálenosti v kilometrech nejsou podložené. Zatímco postupné zmenšování Měsíce subjektivně vnímáme, nadto je zesílené v horách, objekty vzdálené desítky kilometrů dosud stoupat nevidíme. Projevily by nepatrné subjektivní zvětšení nebo ne?

Lze uvažovat o pohledu na velmi vzdálené letadlo na letišti a potom ve stejné vzdálenosti nahoře - totéž letadlo ve výšce.

3. Hledání měřítka

Otázkou je, jak vlastně hodnotit různé vzdálenosti v obrázku. Za základ kroků v diskrétním prostoru se nabízí Planckova délka. Vzdálenost 0-1, značená 0-10 km (obr. 3), značí základní vzdálenost Planckovy délky 1,62·10^-35 metru. Pak ovšem veškeré vzdálenosti, které očima vnímáme, by byly hodnocené na obloucích nesmírně vzdálených. Všechny objekty, i ty pozorovateli nejbližší, by měnily vnímané velikosti tak jako Měsíc.

Jenže my žádné Planckovy délky očima nerozlišujeme. Nabízím, že vzdálenosti oblouků jsou úměrné našim zrakovým možnostem. Hlubší nastudování problematiky je nutné. Vzdálenosti úměrné Planckovým délkám zde nesleduji.

4. Hledání výšky

Zatím neznám kresby zcestovatělých přírodovědců nebo malířů, jak vlastně člověk vnímá stoupající Měsíc na rovníku, na jižní a severní polokouli či na pólech. Nebo jak ve velké výšce, případně na oběžné dráze o výšce stovek kilometrů.

4.1. Na horách

Vjemy se liší na horách a v nížině. Dovolím si další úvahy.

Změním výšku nad vodorovnou osou; pro vycházející Měsíc nebo pro pozorovatele. Měsíc vychází na oblohu z osy x. Umístím pozorovatele nad osu x, do bodu [0,1] (obr. 4). Jeho vnímání vycházejícího Měsíce je to největší, dotýká se osy x.

Obr. 4. Pozorovatel P je umístěný na horách [0,1]

Je takové mimostředné umístění pozorovatele přijatelné? Vždyť má být v počátku souřadnic. Ve středu svého zobrazení. Jenže zde hledám něco nesrozumitelného, proto zkouším další postup, bez zásadní obhajoby.

V práci IV jsem zavedl možnost - spekulaci, že člověk vnímá fotony očima, ale velmi vzdálené objekty z diskrétního prostoru přepočtem z diskrétní databáze o bodech Vesmíru, přímo do vědomí. To dovoluje zkoušet i posuny mimo střed vnímání.

4.2. V nížině

Obr. 5. Nezaručený výhled pozorovatele P v nížině [0,0] na nízký Měsíc

Nezaručím pozorovateli v nížině, v bodě [0,0], že vidí Měsíc už v jeho nejnižší, nezakreslené poloze (obr. 5). Možná vnímá Měsíc až od výšky y = 1, jako oblouk I. A to už je Měsíc zmenšený. I v hledišti bývá výhodnější sedět ve zvýšené řadě, kvůli dobrému výhledu.

Kapitoly 4.1. a 4.2. tak zkoušejí zdůvodnit zážitek obrovského vycházejícího Měsíce, je-li pozorovatel na horách.

5. Závěr

Uvažování v navrženém směru vyžaduje praktické poznatky z posuzování lidských vjemů. Dosavadním nedostatkem, zde sledovaného řešení, je zvětšování Měsíce v zenitu.