Kvadratický - perspektivní zrakový prostor
Jiný prostor, perspektivní - IIv
💾

Bohumír Tichánek
v. 5.11.2023a
* * *
„Je jistě dobré vědět, kam jdete, ale nesmíte zapomínat,
že jediné, co je na vaší cestě reálné, je krok, který děláte
v přítomném okamžiku. Nic jiného neexistuje.“
Eckhart Tolle - Moc přítomného okamžiku
* * *
Práce zkouší matematizovat zrakový perspektivní prostor.
Smyslovému zážitku je dosud věnovaná malá pozornost. Nedoceňujeme
skutečnost, že nezkoumáme hmotu, ale zážitky hmoty - (viz Ernst Mach).
Rovnoměrný růst zvukové energie nevnímá sluch stejným
způsobem, nýbrž hlasitost se zesiluje logaritmickou závislostí.
To musel zjistit experimentátor sám na sobě, na svém sluchu.
Výkon signálu z reproduktoru lze měřit, ale sluchový vjem už
musel člověk určovat svým vědomím.
Ale posuzovat, jak jsou rozložené objekty v geometrickém
perspektivním prostoru zrakového vnímání, je ještě ošemetnější.
Bezvýsledné výpočty rovnic 2D prostoru (rovnice kružnice, Pythagorova věta) svými iracionalitami něco napovídají. Prověřuji odlišnou
geometrii. Perspektivní prostor má vzdálenost každých dvou bodů vždy racionální. Alternativně vysvětluje výstavbu našeho světa.
Je hmota nebo jsou jen vjemy hmoty?
Pojmy
Diskrétní prostor - obsahuje rozlišené body. Jejich souřadnice jsou výhradně
celočíselné a vzdálenosti se určují počtem svislých a vodorovných
kroků. Délka kroků se nehodnotí, jen počet. Takovým prostorem je i šachovnice.
Kvadratický prostor -
osové souřadnice Euklidova prostoru má umocněné na druhou.
Perspektivní prostor - je
daný zrakovým i sluchovým vnímáním člověka.
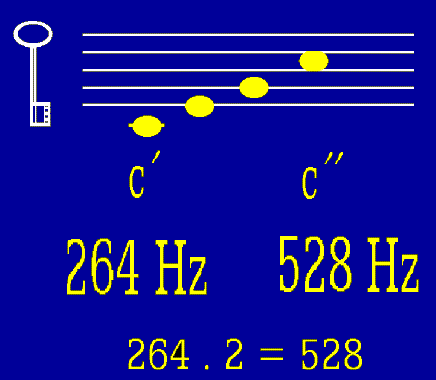
Obr. 1.
Více jsou akceptovány takové obory poznání, které jsou
matematizovatelné. Kupodivu je v souladu s tímto vědeckým
požadavkem i hudba. Celá stupnice, oktáva, má poměr kmitočtů
prvního a posledního tónu 1:2. Příjemný sluchový zážitek tuto
výpočetní souvislost dobře potvrzuje. Rovněž hudební akordy dbají
podobných výpočetních poměrů.
««« SLEDOVAT VŠECHNY OBRÁZKY I V LEVÉM SLOUPCI
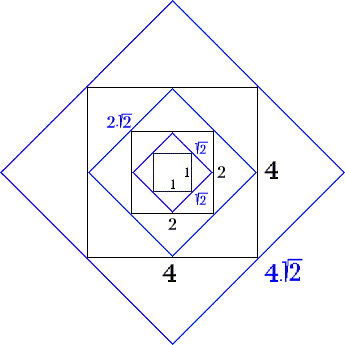
Obr. 2.
Euklidovu prostoru byl zaveden další druh čísel - iracionální,
např. odmocnina ze 2. Matematika byla obohacena - ad hoc.
Avšak z hlediska Occamovy břitvy to není úspěchem poznání světa.
Neboť cennější je, když problematiku vysvětlíme - v její úplnosti
- menším počtem zásad.

Obr. 3.
Fyzika nesleduje matematický popis geometrie zrakového zážitku.
Prostor s perspektivou nemá lineární přírůstky délky, jaké obrázek
zapisuje. Není snadné popsat to, co máme ve vědomí.
„Závislost sil na vzdálenosti lze zjistit experimenty,
ale závislost geometrických vztahů na vzdálenosti lze jen
předpokládat.“
Nikolaj Ivanovič Lobačevskij
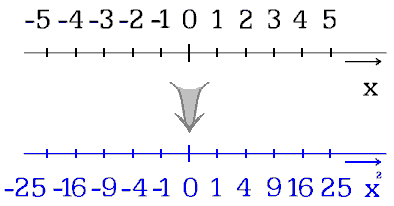
Obr. 4.
Ověřuji perspektivní prostor užitím kvadraticky cejchovaných os.
Řada přirozených čísel byla umocněna na druhou. Tím zkouším
vystihnout rozmístění zrakových zážitků. Kulový prostor, v němž ubývá rozměrů od středu koule k jejímu
povrchu, studoval Hermann Helmholtz v 19. století a jiní.
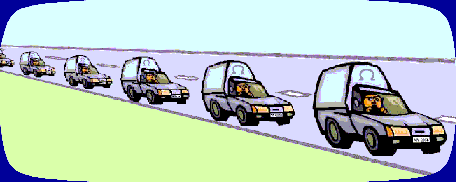
Obr. 5.
Perspektivní prostor předává tvoru víc podrobností z blízkosti
než z dálky. Zdůraznění blízkých jevů napomáhá přežití tvora.
Ovšem takové souvislosti se dosud zdůrazňují pro biologii a ne pro
geometrii lidského působiště - pro svět.
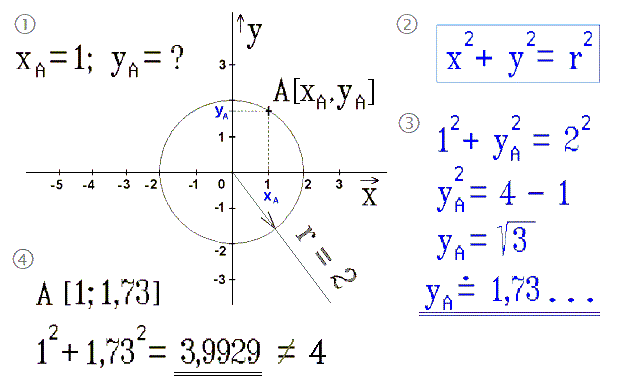
Obr. 6.
Bod na kružnici je zadaný jednou souřadnicí xA.
V Euklidově prostoru mu nelze vypočítat umístění druhé souřadnice
yA. Zaokrouhlení dle požadované přesnosti
je technice dobře přijatelné, jenže věda používá matematický popis světa, který je někdy
nepřesný.
Jen málokdy se objevují námitky proti iracionálním vzdálenostem.
Doporučí se jejich vyjádření nekonečným rozvojem. Jenže na
chybějícím výsledku to nic nezmění.
Iracionality překážejí popisu konstrukce našeho Vesmíru.
Geometrická vzdálenost je konečná, ale nekončící výpočet ji
nevystihuje. Vlastnosti téže
veličiny, v matematice a v geometrii Euklidova prostoru, jsou v rozporu.

Obr. 7.
Prostředí s kvadraticky rozloženým prostorem je snadno matematizovatelné. Výpočet chybějící souřadnice bodu
na kružnici má úplnou přesnost! Výsledkem můžou být čísla necelá, avšak lineární rovnice žádné iracionality nevnášejí.
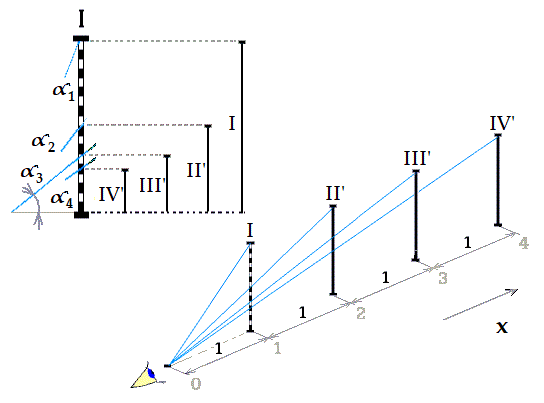
Obr. 8.
Euklidův prostor posuzuje výšku objektů velikostí zorného úhlu.
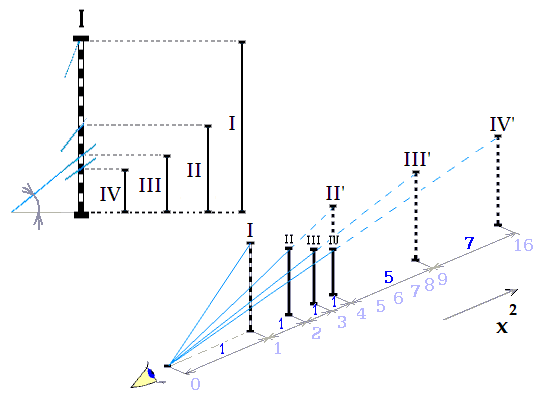
Obr. 9.
Také kvadraticky rozložený prostor zobrazí zrakové zážitky
stejným zorným úhlem. Náš svět netřeba vysvětlovat
zrovna tím nejobvyklejším - Euklidovým prostorem (obr. 8).
Zážitky můžou být do vědomí přenášené hotové - jako kvadraticky
stlačené (obr. 9). Vznik těles ze zrakových zážitků
neodporuje názoru Ernsta Macha a snad ani kvantové mechanice.
Vesmír je takto daný přímo perspektivními zrakovými
zážitky, promítanými do vědomí bez Euklidova prostoru.
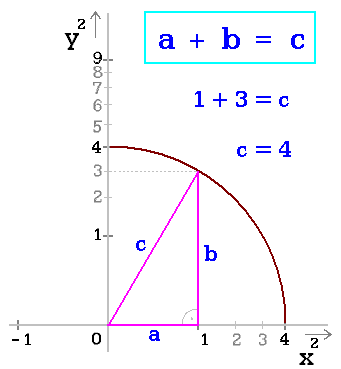
Obr. 10. Linearizovaná Pythagorova věta
Perspektivní svět předkládá nevyvratitelné zrakové zážitky a
navíc jeho matematika nenachází v pravoúhlém trojúhelníku
iracionální čísla. Konečnou vzdálenost mezi dvěma body sdělí
číslem konečné velikosti. Zrakové vjemy jsou nám základní, proto sledujme jejich původ.
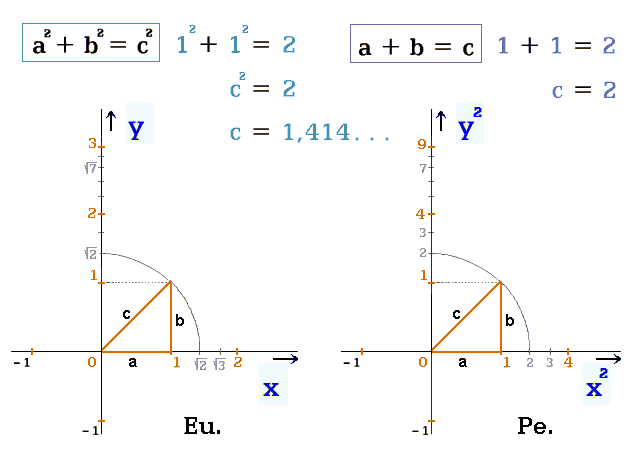
Obr. 11. Porovnání
Osy lineární, rovnice kvadratická:
a2 + b2
= c2.
(obr. 11 vlevo)
Osy kvadratické, rovnice lineární:
a + b = c.
(obr. 10, obr. 11 vpravo)
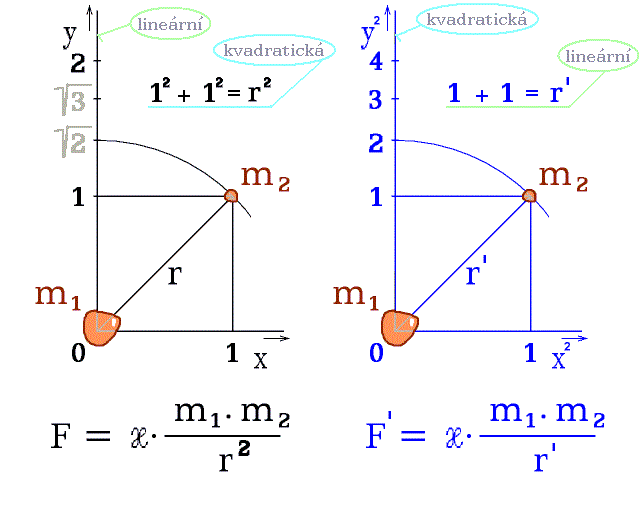
Obr. 12.
Porovnání výpočtu síly, podle Newtona, ve dvou odlišných
geometrických prostorech. Hmotnosti jsou m1
a m2. Rovnice perspektivního prostoru je
lineární: vzdálenost r' je v první mocnině.
Barevnými ovály zdůrazňuji prohození kvality „kvadratická“ -
„lineární“ mezi oběma prostory, mezi rovnicí a cejchováním os.
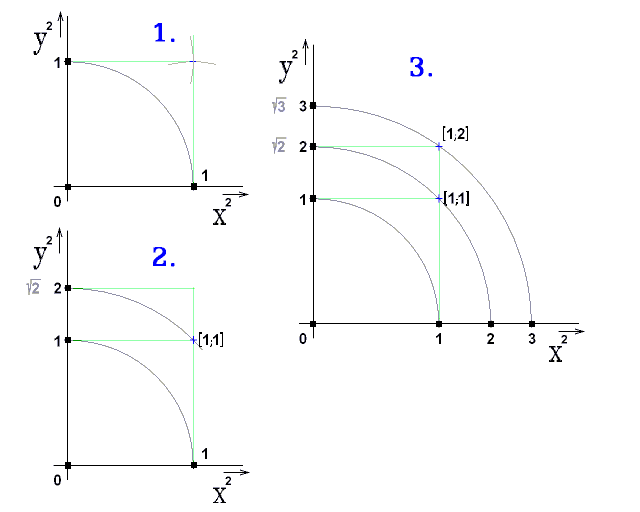
Obr. 13.
K ocejchování os kvadratickým měřítkem postačí kružítko s pravítkem.
Prostor
|
Euklidův |
Perspektivní |
| Délka 1D |
racionální či iracionální |
racionální |
| Hodnověrnost |
tradice od Pythagora |
smyslový zážitek |
| Matematizovatelnost |
až dohodou o nových číslech |
splňuje
|
| Řád rovnic |
kvadratické |
lineární |
| Převod z diskrétního |
ne |
ano |
Tab. 1. Srovnání prostoru perspektivního a Euklidova
lineárního
Snadná matematizace perspektivního prostoru nabízí, že skutečný
svět je daný právě našimi smyslovými zážitky. Za ním nacházím prostor z oddělených bodů 1).
Uvažuji nejen perspektivní geometrický prostor, ale i perspektivní čas. To opravňuje transformovat rovnici
E = mc2 na E = mc, v perspektivě. Rozvíjím v práci o speciální teorii relativity 2).
1) IIIv - převod bodů diskrétního prostoru do kvadratického prostoru
2) STR-VIIv - Definice diskrétního času. Převod do
spojitého časoprostoru. Perspektivní čas. Zdůvodnění zpomalovaného času při pohybu.
Růst relativistické hmotnosti. Atd.


