Obr. 1.

Již po několik staletí exaktní vědy neuvažují jen Euklidův lineární spojitý prostor, nýbrž teoreticky připravily a i prakticky Vesmíru uvažují další prostory - neeuklidovské.

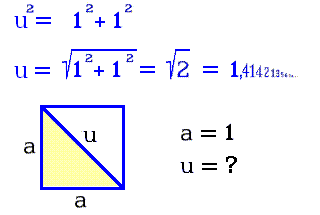
Obr. 2.

Námitka: geometrická vzdálenost mezi protějšími vrcholy jednotkového čtverce je konečná a přesto je její výpočet bez konce! Iracionální výsledek neposlouží, nýbrž řešitel si vybere některé racionální číslo jako nepřesný výsledek. Například 1,4.

Čísla buď racionální nebo iracionální sdělují vzdálenosti v Euklidově světě nebo i v zakřivených prostorech. Jenže dvě úsečky se liší výhradně kvantitativně, kdežto kvalitu mají jedinou - proč tedy dva druhy čísel?

Obr. 3.

Pokračujícím výpočtem se počítaná délka stále jen upřesňuje, například prodlužuje. Výsledek nevznikne!

Obr. 4.

Spojité čtyřrozměrné krychle, různě zdůrazněné. Svými smysly ve světě nezjišťujeme nejen ji, ale ani 3D objekty nevidíme v Euklidově prostoru. Lineární spojitý prostor je hypotézou, zrak jej neukazuje.

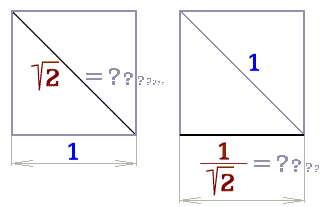
Obr. 5.

Nesouměřitelnost. Po výpočtu Pythagorovou větou se někdy udává vzdálenost jako racionální, jindy iracionální, aniž by se na ostatních fyzikálních vlastnostech bodů nebo vzdálenosti v prostoru něco změnilo. Toto matematické vyjádření zkusím prověřit.

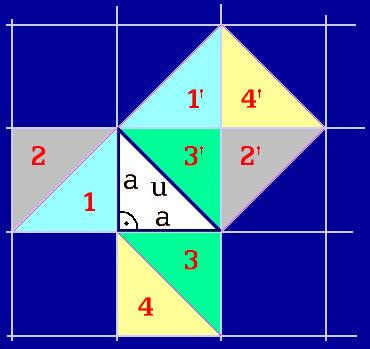
Obr. 6.

Pythagorova věta ve čtvercové síti. Součty obsahů malých čtverců mají být rovny obsahu velkého čtverce:

Výpočet úhlopříčky čtverce je vždy iracionální, to je bezvýsledný. Potom každý výpočtář může zvolit jinou délku, jinak ji zaokrouhlit.

My si ve své mysli představujeme, že všech devět trojúhelníků má stejnou velikost. Podceňujeme svůj perspektivní vjem. V dalším pokračování se pokusím o matematizaci perspektivního zrakového prostoru. S představou o změně výpočtu úhlopříčky.

Hmat snad zaručuje skutečnost? Chodec - středový pozorovatel, má každý další krok opět první. Tím stále zůstává v počátku stlačených souřadnic perspektivního prostoru. Můžeme přísahat, že svět má lineárně rozloženou hmotu?

Vybírám mezi dvěma možnostmi. Hledaná odmocnina je buďto číslem - anebo pokynem k hledání čísla: najdi číslo, které násobené samo sebou dá dvě! Matematika pracuje s číslem jakoby nalezeným. Jejím upřednostňováním se podceňují možné postupy k vyřešení nesrovnalosti, vyjádřené 3. obrázkem. Bylo by možné upřesnit geometrické názory na svět, ve kterém žijeme?

Obr. 7. Různoběžky či rovnoběžky (podle www.gymfry.cz)

Názor Ernsta Macha: zvláště fyzika získá největších vysvětlení od biologie, a to analýzou smyslových počitků [1].

Vycházel z názoru, že objektem vědy jsou komplexy počitků, které nemají objektivní příčinu. Matematika vznikla ze smyslových zážitků. I když až jejich abstrakcí. Fyzikální poznatek o teplotě hrnku s vřelou vodou lze někdy zjistit i bez přemýšlení, kdežto zjistit počet hrnků vyžaduje abstrahovat.

Zjišťuji jakousi nesnáz pro závěry filosofa K. Poppera. Na jedné straně bývají smyslové zážitky ovlivněné chybami. Například hledíme na obraz rovnoběžek, ale máme mylný pocit, že jsou to různoběžky (obr. 7). Nejmenší detaily určují naše rozhodnutí. Až zkoumáním detailů přibližujeme skutečnost, ne jejich zanedbáním.

Filosof Karl Raimund Popper poučil - předpokladem vědeckého pokroku je vyvratitelnost přijímaných poznatků. Nevyvratitelné názory věda nejen odmítá, ale někdy jimi lidé i opovrhují. Jenže naše nevyvratitelné smyslové zážitky jsou základem poznání.

Kde, v jakém prostoru hledáme zdůvodnění fyzikálních poznatků? Kde hledáme svůj život?

Literatura

[1] Kantova filosofie ve svých vztazích k vědám exaktním - Karel Vorovka. JČMF, Praha 1924, s. 119