Příčina zpomalování času. Jeho ztotožnění
💾

Bohumír Tichánek
* * *
OBSAH
0. Úvod1. Použité termíny
2. Životní působiště prostor, čas a hmota
3. Euklidův prostor
3.1. Dvě posouzení linearity světového prostoru
3.1.1. Hmat
3.1.2. Zrak
3.2. Nahradit Euklidův prostor
4. Perspektivní prostor
4.1. Zrakové souvislosti
4.2. Cejchování os perspektivního prostoru
4.3. Matematizace perspektivního světa
4.4. Ověření perspektivy zorným úhlem
5. Perspektivní prostor kompatibilní s diskrétním
5.1. Provedení bodového prostoru
5.2. Bodový prostor k iracionalitám
6. Ke Speciální teorii relativity
7. Hledání souměrného diagramu, který zobrazí rovnocennost času a délky
7.1. Konstrukce k souměrnému diagramu Euklidova prostoru
7.2. Z prostoru Euklidova do perspektivního
7.3. Nelineární časový průběh
7.4. Převod perspektivní kružnice do diskrétního prostoru
8. Příčina vzniku diskrétní kružnice v časoprostoru
8.1. Poloha tvora N v časoprostoru
9. Pulsace
9.1. Pulsy časové, délkové a silové
9.2. Rychlost světla
10. Časoprostor pulsního Zdroje
11. Diskrétní a perspektivní diagram
12. Převod z diskrétního prostoru do perspektivních a Euklidovských souřadnic
13. Uplatnění času
13.1. Podstata času
13.2. Přítomnost
13.3. Současnost
13.4. Mion
13.5. Kruhový pohyb
14. Shrnutí
15. Možný přínos zde představeného mechanického modelu
16. Zdroje
0. Úvod
Diskrétní prostor tvoří posice pro uskladnění informatických bodů. Tyto body se přesunují do sousední posice výhradně na povel časové základny - Zdroje pulsů. Tvoří veškerou látku Vesmíru. Dávají vzniknout jak času, tak i pohybu.
Zavedený hypotetický taktovací Zdroj opakuje své pulsy, a tím stále znovu nabízí přesun bodů. V jednom pulsu bod neuskuteční víc pohybů; vykoná buďto jediný nebo žádný přeskok z posice do sousední posice. Úhlopříčný pohyb bodů mezi dvěma posicemi není zaveden. Pokud bod přeskakuje v každém dalším pulsu Zdroje, pak letí rychlostí světla.
Diskrétní časoprostor nepřevádím do Euklidova prostoru, nýbrž rovnou do zrakové i sluchové perspektivy. Převod z diskrétního do perspektivního prostoru, který vnímáme, ať koná hypotetický procesor. Pulsace diskrétního podložení takto podmiňují jevy spojitého časoprostoru.
O pohybu rozhoduje Informatický Procesor. A to podle vlivu dosavadních veličin; vnější síly (gravitace, apod.) a i setrvačnosti v pohybu látky. Jistý vliv způsobí, že bod na povel pulsu nereaguje. Zůstává v posici.
Práce sleduje exaktní základy a to šetřením zaokrouhlovaných
iracionalit a také postulátů teorie relativity.
1. Použité termíny
1.1. Informatický bod … informace 1 bitu o obsazení posice. Ta je buď obsazena nebo neobsazena
1.2. Posice … úložiště pro informaci 1 bitu. Je funkčně provázaná s dalšími posicemi. Například v 3D prostoru s šesti jinými okolními posicemi. Umožní bodu přesunout se, do jedné z nich, na povel pulsu
1.3. Perspektivní prostor … geometrický prostor, jenž vystihuje zrakové vnímání. Je odvozený z kartézského prostoru, jehož lineární cejchování os má umocněné na druhou
1.4. Zdrojový puls [PE]… Výsledek činnosti Zdroje, nutný k přemísťování informatických bodů
1.5. Zdroj = časová základna … vytváří sled pulsů [PE], jimiž se ovládají posice. Některé body využijí pulsy k přeskoku do sousední posice. Foton, chápaný zde jako bod, přeskakuje při každém dalším pulsu
1.6. Pohybový (délkový) puls [PL] … v něm bod přeskočí do sousední posice
1.7. Silový puls [PF] … Změní dosavadní pohybový stav bodu. Například upraví jeho předchozí rychlost 0,1 posice/puls (1 posice/10 pulsů) na jinou, čímž změní předchozí ustálené střídání pulsů pohybových a časových
1.8. Časový puls [PT] = puls (diskrétního) času … ten puls Zdroje, v němž uvažovaný bod neopouští svou posici, ani není pulsem silovým
1.9. Diskrétní čas [PT] … součet počtu pulsů, nevyužitých k přesunu bodu do sousední posice
1.10. Perspektivní čas [s2] … Kvantita perspektivního času [s2] je rovna kvantitě diskrétního času [PT]. Tvor ji však vnímá stlačenou kvadratickým přepočtem
1.11. Čas (lineární) [s] … newtonovská nebo relativistická veličina, daná odmocninou ze součtu pulsů [PT]
1.12. Souměrný diagram … zobrazí vzájemnou závislost času a prostoru. Odvozený postupně z Lorentzova zpoždění času a z rovnice kružnice, vytvořený v prostoru diskrétním a perspektivním. Osa svislá je časová a vodorovná je délková
1.13. Kružnice souměrného diagramu … rostoucí, nahrazuje vodorovnou stoupající přímku Minkowského diagramu
1.14. Současnost … proces nabízející všem posicím, v zavedeném diskrétním prostoru, přemístit body účinkem téhož pulsu
1.15. Přítomnost … fyzikálně podmíněný pocit existence. Vede k němu perspektivní zpracování veličin časoprostoru. Příčinu pocitu přítomnosti nabízí časový úsek při počátku souřadnic, protože je ze všech úseků nejdelší
1.16. Perspektivně stlačený časoprostor … má vodorovnou délkovou a svislou časovou osu s cejchováním kvadratického průběhu
1.17. Vesmírný procesor …
přepočítává body prostoru diskrétního do perspektivního
vnímání
2. Životní působiště prostor, čas a hmota
Prostor – nejpřesněji lze užívat perspektivní prostor, protože má jen racionální čísla.
Čas – pulsace vyjasňuje jeho definici, vzhledem k jeho závislosti na pohybu. Také příčinu zpožďování času v STR při pohybu.
Hmota je daná informatickými vjemy, přímo do vědomí.
Svět je tak virtuální realita.
3. Euklidův prostor
Technika zanedbává nepatrné zbytky veličin, jimiž se její konstrukce neovlivní - iracionality.
Rovněž věda – fyzika může obdobně opouštět drobnosti
Euklidova prostoru. Profesor Rudolf Zahradník se mi před lety
v dopisu vyjádřil [1]:
„Váš odpor k iracionálním číslům mně trošku (zcela formálně, ovšem) připomíná odpor některých k přibližnému řešení diferenciální rovnice (které ovšem mohu hnát k libovolné přesnosti); já mám z něho naopak radost, protože z hlediska přírodovědeckého či technického je to stejně užitečné, jako řešení přesné.“
Práce bez iracionalit směřuje k přesnosti, kterou ani dnešní věda neužívá; blíž samotnému základu exaktních věd.
Nalezení přesného vyjadřování fyzikálních veličin, bez
iracionalit; to může přiblížit výstižnější hodnocení světa. Je
původním úkolem vědy – poznávat, kde to žijeme.
3.1. Dvě posouzení linearity světového prostoru
3.1.1. Hmat
- pozorovatel vždy znovu udělá další krok a krajina mu ubíhá rovnoměrně. Usoudí na linearitu.3.1.2. Zrak
- pozorovatel vždy znovu udělá první, a nikdy další krok. Stále zůstává v počátku souřadnic perspektivního prostoru a jeho vždy prvním krokem mu krajina rovněž ubíhá rovnoměrně. Má stejný argument, jaký dává hmat. A přitom chystané druhý a další kroky mu naznačují, že se nachází v nelineárním perspektivním prostoru.3.2. Nahradit Euklidův prostor
Hmotu, rozmístěnou jakoby v Euklidově prostoru, hodnotíme v našich představách. Smysly lineární prostor nevnímají, a jeho matematizace se nedaří. Vždyť výpočty většinou bývají bezvýsledné – iracionální.
Proto zde nepoužiji Euklidův svět s jeho rozmístěnou hmotou. Zrakové obrazy ať jdou do vědomí, vnášené Informatikou – namísto představy o hmotě v prostoru, jež vysílá světlo. Veškeré smyslové informace může do vědomí dávat hmota, anebo Informatika.4. Perspektivní prostor
4.1. Zrakové souvislosti
Zrak dává, ze všech smyslů, lidskému prostorovému poznání nejvíc informací [bit]. Pohled je perspektivně zkreslený vždy jinak, dle přemísťování po Zemi. Opouštím názor o vzniku perspektivního vjemu skrz zorný úhel objektů; a uvažuji jinak.4.2. Cejchování os perspektivního prostoru
Ocejchování perspektivního prostoru na osách řeším přepočtem. Umocněním souřadnic kartézského prostoru na druhou (obr. 1).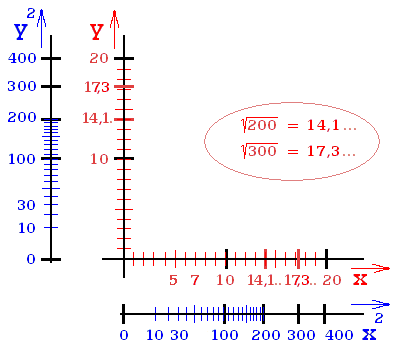
Obr. 1. Cejchované osy Euklidova a perspektivního prostoru
««« SLEDOVAT VŠECHNY OBRÁZKY I V LEVÉM SLOUPCI
4.3. Matematizace perspektivního světa
Lineární Euklidův prostor používá kvadratickou Pythagorovu větu: a2 + b2 = c2
a, b, c … strany pravoúhlého trojúhelníka
Následně prostor s kvadraticky přepočtenými souřadnicemi vyžaduje opačně, lineární tvar Pythagorovy věty (obr. 2). Lineární rovnice nemá iracionality: a + b = c
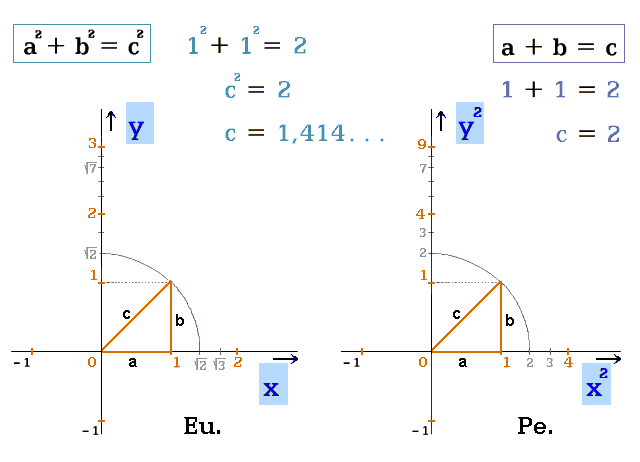
Obr. 2. Pythagorova věta v matematice a v geometrii, prostor Euklidův [x, y] a perspektivní [x2, y2]
4.4. Ověření perspektivy zorným úhlem
Zorný úhel ověřím v obou prostorech; dvěma obrázky, vždy s nakreslenými čtyřmi sloupky.
Euklidův prostor. Hmotné sloupky označuji I, II’, III’, a IV’. Jejich výšku posuzuji velikostí zorného úhlu a to na I. sloupku (obr. 3). To je způsob úměrný zobrazení na oční sítnici. Tyto sloupky míváme za skutečné, vytvořené ve hmotě.
Obr. 3. Sloupky v Euklidově prostoru
Obr. 4. Sloupky v perspektivním prostoru
Perspektivně rozložený prostor zobrazí zrakové zážitky stejným zorným úhlem (obr. 4).
Zorný úhel vyhovuje oběma prostorům.
Zmenšující se perspektivní sloupky II, III a IV nejsou domněnkou, nýbrž jsou nevyvratitelným smyslovým zážitkem.
Naopak otázný je Euklidův prostor, který
a) nevnímáme,
b) obsahuje jen přibližnou matematizaci – nepřesné,
neupřesnitelné iracionality.
5. Perspektivní prostor kompatibilní s diskrétním
Diskrétní (bodový) prostor navazuje na perspektivní prostor. V obou prostorech má každý bod své parametry stejné: vzdálenost od počátku a obě souřadnice (obr. 5).

Obr. 5. Diskrétní prostor kompatibilní s perspektivním
Prostor diskrétní se nabízí být základem, z něhož se body přepočítávají do perspektivního vnímání. Počátkem je místo, odkud tvor vnímá své okolí. Přepočet ať zajišťuje hypotetický Vesmírný procesor.
Pozorovatel se nachází v bodě K a potom J (obr. 6). Perspektiva poskytla odlišně zprohýbané vjemy, kdežto skutečnost je v diskrétním prostoru.
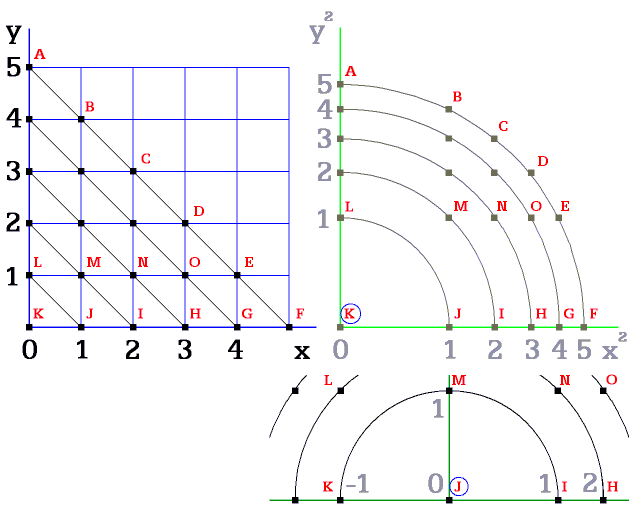
Obr. 6. Každý pozorovatel je středem svého systému
5.1. Provedení bodového prostoru
Bodový prostor ať je databází pro veškerou látku. Některé posice prostoru jsou obsazené body, a jiné jsou prázdné. Vzdálenost mezi body se nedefinuje. To až ve spojitém prostoru můžeme přidělit informatickému bodu zjištěnou Planckovu délku. Také Planckův čas, pro přeskok do sousední posice.
Čtverec, postavený na vrchol, je vytvořený z bodů, které mají shodnou vzdálenost od středu (obr. 7). Po překreslení do perspektivy vytvoří kulatou kružnici.
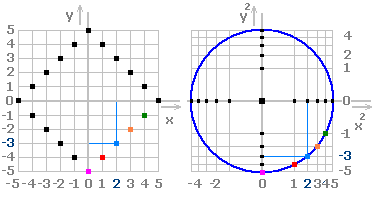
Obr. 7. Bodový čtverec postavený na vrchol je kružnicí diskrétního prostoru
5.2. Bodový prostor k iracionalitám
Ani odmocniny vyššího řádu neznamenají vznik iracionality, když vezmu za příklad krychli. Nevyskytne se objem krychle, který by po třetím odmocnění nedal přirozené číslo. Délka hrany jiné možnosti vylučuje, neboť je vždy zavedená přirozeným číslem v bodovém prostoru.
Ovšem je nutno hledat hlouběji, ohledně nalezení smysluplných
fyzikálních výpočtů odmocnin, jež by vedly k iracionalitě.
6. Ke Speciální teorii relativity
Hermann Minkowski zvýraznil propojenost času a pohybu; založil pojem časoprostoru (obr. 8). Speciální teorie relativity však neobsahuje diagram, který by ukázal rovnocennost času a délky, kterou nauka vyhlásila.Obr. 8. Minkowského graf. Hvězdolet urazil 300.000 km za tři pozemské sekundy
7. Hledání souměrného diagramu, který zobrazí rovnocennost času a délky
Mějme dvě soustavy, první je bez pohybu a druhá se od ní vzdaluje.
{1} Přepočet času mezi dvěma soustavami
t = t0/√(1 – v2/c2)
{2} Upravená rovnice {1}
(t0/t)2 + (v/c)2 = 1
{3} Rovnice kružnice
x2 + y2 = r2
v … rychlost vzdalovaného objektu [m/s]
t … zpomalený relativistický čas trvání děje na vzdalovaném objektu [s]
t0 … čas trvání děje v soustavě, která je bez pohybu [s], t0 < t
c … rychlost světla [m/s]
x, y … souřadnice bodu [-] na dvou osách diagramu
r … poloměr kružnice [-]
7.1. Konstrukce k souměrnému diagramu Euklidova prostoru
Dvěma příklady, (1) a (2), získám souřadnice dvou bodů, které patří hledanému souměrnému diagramu. Druhá soustava se bude vzdalovat od první nejprve rychlostí minimální (1) a potom maximální (2).
• Příklad (1)
Druhá soustava se vzdaluje od první soustavy nulovou rychlostí v = 0. Následně v rovnici {2} jsou shodné časy t = t0. Pak ve {3} druhý sčítanec y = 0 a levý sčítanec x = 1.
Do diagramu získávám bod o souřadnicích [1; 0].
• Příklad (2)
Druhá soustava se vzdaluje světelnou rychlostí, je to foton, v = c. Pak v {2} pravý sčítanec v/c = 1, následně v levém sčítanci pro čas se děj prodlužuje, nekončí, t → ∞. Do diagramu patří bod [0; 1].
Vznikl diagram, v němž sčítance t0/t a v/c, užité v {2} nejsou časem, ani rychlostí. Jsou bezrozměrné, jako i jejich součet 1 [-].
Čtvrtkružnice podle {3}, o poloměru 1, má vypočtené dva body (obr. 9).
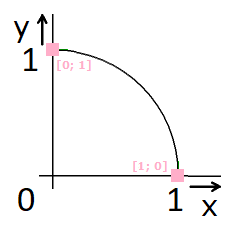
Obr. 9. Čtvrtkružnice Euklidova prostoru
7.2. Z prostoru Euklidova do perspektivního
Prostor Euklidův [x; y] nahradím perspektivním [x2; y2] (obr. 10, 11). Rovnice kružnice {2} se změní na {4}.
{2} (t0/t)2 + (v/c)2 = 1… rovnice kružnice Euklidova prostoru
{4} t0/t + v/c = 1 … rovnice kružnice v perspektivě
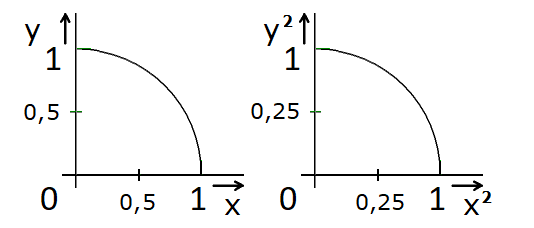
Obr. 10. Čtvrtkružnice prostorů Euklidova [x; y] a perspektivního [x2; y2]
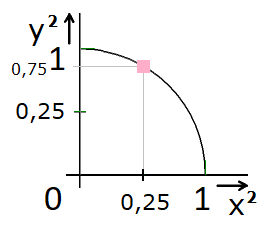
Obr. 11. Na čtvrtkružnici perspektivního prostoru leží např. bod [0,25; 0,75]
Nelineární délkový prostor je snadno přijatelný; je to smyslový zážitek zraku a sluchu. Je však nutné užít i nelineární průběh času; to si žádá potřeba transformace a to z Euklidova do perspektivního časoprostoru.
7.3. Nelineární časový průběh
Ručka hodin přeskakuje ciferník po 1 sekundě, ukazuje lineární čas. A přece lze hledat podobnost s opakovaným prvním krokem při chůzi. Věříme v lineární Euklidův prostor, ačkoliv matematika nabízí – perspektivní prostor s racionálními výpočty (podle Occama je lepší, protože snižuje počet zavedených druhů čísel). Nabízí se nám informatický svět, zdánlivá skutečnost.
Vždy znovu jsme v přítomnosti, podobně s kapitolou 3.1.2. Je nepodložené, když vyvozujeme z neustále stejných prvních úseků názor lineárního času.
Jinak by bylo ve spojitém prostoru, kde názor na úseky by byl
stěží obhajitelný.
7.4. Převod perspektivní kružnice do diskrétního prostoru
Podle 5. kapitoly jsou kompatibilní diskrétní a perspektivní prostor.
Časový rozdíl mezi dvěma fyzikálními soustavami sleduje výše
zavedená rovnice {4}: t0/t + v/c = 1.
Avšak ani tato rovnice kružnice perspektivního prostoru
nevysvětluje příčinu fyzikálního chodu Vesmíru – časoprostoru.
Perspektivní časoprostor navazuji na Minkowského diagram. Proto na vodorovné ose roste prostorová délka, a na svislé postupuje čas soustavy, která je bez pohybu (obr. 15).
V perspektivě je čtvrtkružnice o poloměru r = 5 (obr. 12).
Všechny její souřadnice přebírá beze změny bodová úsečka.

Obr. 12. Kompatibilita diskrétního a perspektivního prostoru
8. Příčina vzniku diskrétní čtvrtkružnice v časoprostoru
V diskrétním prostoru zvolím fyzikální veličinu, která zajistí nutný růst perspektivní kružnice a zvedání polopřímky Minkowského diagramu. Vznik času i pohybu. Což ve spojitém prostoru nebylo zdůvodnitelné v osách x2, y2 nebo x, y.
Zdroj (dosud hypotetický) opakovaně zásobuje diskrétní prostor pulsy, které značím 1 PE. Puls vytvoří v posici informatický bod. Úkolem pulsací Zdroje jsou přesuny bodů do dalších posicí. Tedy pohyb látky ve Vesmíru. Každým dalším pulsem bodovou úsečku pokaždé prodlouží o 1 posici (obr. 13). Časoprostor roste.
Šikmé bodové úsečky 1D geometrického prostoru (Diskr.) jsou překresleny do perspektivního vnímání tvora (Kont.), který by byl v počátku souřadnic (obr. 13). I když tam nikoho neumísťuji; vždyť líný tvor je přesunován nahoru po časové ose časoprostoru. Přibývá mu čas.
Diskrétní časoprostor roste zásluhou pulsace Zdroje. Každý bod - tvor se vždy nachází na některé šikmé bodové úsečce časoprostoru, teoretického pojmu.
Ohledně umístění tvora ve světě – tvor je vždy
k nalezení na vodorovné ose 1D geometrického prostoru,
který obývá.
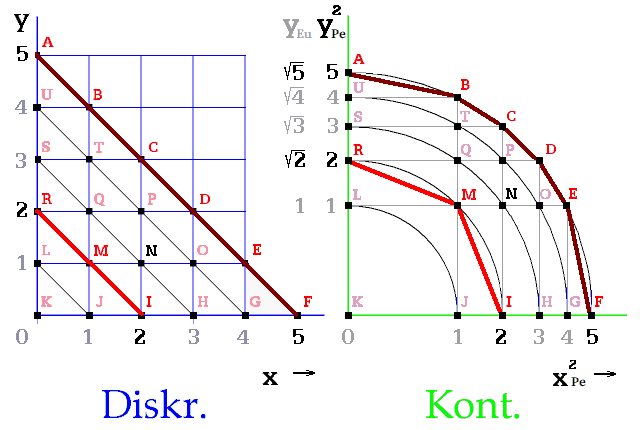
Obr. 13. Časoprostoru opakovaně narůstá bodová úsečka
Příklady (3), (4) a (5) pro 2D časoprostor (obr. 13):
(3) Ať bod K přeskakuje stále vpravo, je to foton. Pátým pulsem je v posici F.
(4) Ať bod K se opozdí. Nejprve nereaguje, tzn. naskočí mu čas do posice L. Potom rychlostí c obsazuje posice M, N, O, E. Po každém dalším pulsu vždy byl na obvodě rostoucí kružnice.
(5) Bod K nereaguje na žádný z pěti Zdrojových pulsů PE. Do posice A ho dopravilo 5 PT.
8.1. Poloha tvora N v časoprostoru
V časoprostoru (obr. 13) tvor přeskákal z posice [0; 0] do posice [2; 1], bod N. Potřeboval na to 3 PE.
Rozmístění bodů v jeho novém perspektivním okolí, po třetím PE (obr. 14).

Obr. 14. Perspektivní časoprostor bodu N
8.2. Význam délkové osy x2
Vodorovná osa souměrného časoprostorového diagramu přímo nevyjadřuje délku fyzikálního prostoru.
Šikmá úsečka diskrétního provedení, tak jako čtvrtkružnice, pravidelně roste zásluhou pulsace Zdroje.
Jenže, pokud se tvor 1D prostoru pohybuje doleva, pak by v zavedeném grafu vystoupil z rostoucí časoprostorové šikmé úsečky. To odporuje jejímu zavedení.
Vodorovná, délková úsečka souměrného diagramu ať vyjadřuje počet uskutečněných délkových pulsů PL. Bez ohledu na směr pohybu tvora v 1D prostoru.
9. Pulsace
9.1. Pulsy časové, délkové a silové
Pohyb fotonu vyžaduje, aby každý Zdrojový puls PE jej posunul do sousední posice po délkové ose. Zdrojový puls PE zde získává funkci pohybu: pohybový (délkový) puls 1 PL.
Přeskok bodu po svislé ose časové označím 1 PT – časový puls. Příležitost k pohybu bodu v našem světě nebyla využitá, proto se zážitky hmoty tímto pulsem vůbec nezměnily. Absenci pohybu sleduji na vodorovné ose.
Střídavé využití pulsů PL a PT určuje pomalejší pohyby hmoty v časoprostoru.
Silový puls PF mění pohybový stav bodu – viz kapitola 1.7.
Použité termíny.
9.2. Rychlost světla
Pohyby ve Vesmíru mají jedině rychlost světla, při hodnocení bodů mezi posicemi. I pomalé pohyby značí přeskoky bodu vždy rychlostí c = 1PL/PT, doplněné velkou dobou nečinnosti mnoha PT.10. Časoprostor pulsního Zdroje
V diskrétním časoprostoru se šikmá bodová úsečka vzdaluje počátku. Prodlužuje se každou další pulsací vždy o 1 posici. Bodová úsečka ať je jedním rázem posunutá do sousedních posicí. V diagramu Minkowského jí odpovídá stoupající polopřímka.
V časoprostorové vzdálenosti 20 PE od počátku umísťuji tři objekty: postavu, koráb a foton (obr. 15).
Postava na svislé ose prožila bez pohybu 20 PT, foton na vodorovné ose získal 20 PL a koráb v poloviční diskrétní rychlosti světla střídal časové a délkové pulsy PT a PL (obr. 15).

Obr. 15. Využití 20 PE v diskrétním prostoru
11. Diskrétní a perspektivní diagram
Obr. 16. Časoprostor diskrétní. Stav po vytvoření 2×1050
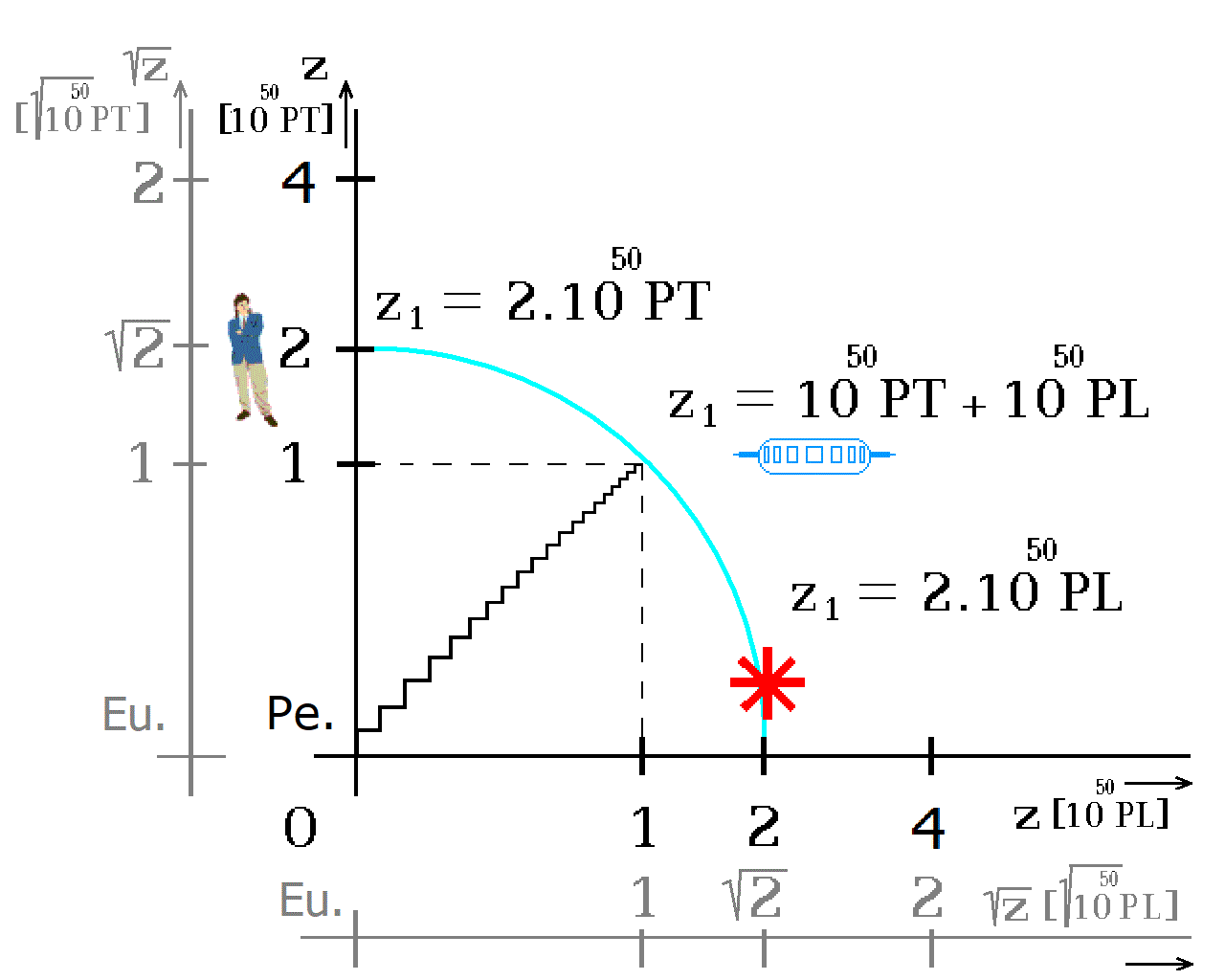
Obr. 17. Časoprostor perspektivní a Euklidův
Výukový obrázek ukazuje postavu na časové ose v diskrétním čase 2×1050 PT (obr. 16). Přitom foton je ve vzdálenosti 2×1050 PL. Kosmoplánu jsou rozděleny Zdrojové pulsy na polovice 1050 PL a 1050 PT.
Převod z diskrétního do spojitého prostoru řeším perspektivně
stlačenými souřadnicemi délkovými a časovými (obr. 17).
Vzniká perspektivně stlačený časoprostor. Perspektiva užije
stejná čísla jako diskrétní prostor, například 1050 PL,
ovšem člověk tu délku vnímá nelineárně.
12. Převod z diskrétního prostoru do perspektivních a Euklidovských souřadnic
Diagram převádí údaje z diskrétního do perspektivního prostoru [km2, s2]. Obsahuje i Euklidovské cejchování [km, s], v němž čas a délka vzniknou odmocněním perspektivních hodnot (obr. 18).
Zde nevkládám Planckův čas a délku, nýbrž výukovému účelu zvolím: 10 PT tvoří 1 s2. Obdobně s délkovými pulsy: 10 PL tvoří 300.000 km2.
Obr. 18. Spojité perspektivní vnímání s vyznačením rastru. (10 pulsů ať zde tvoří 1 s)
13. Uplatnění času
13.1. Podstata času
Nelineární čas je podmíněn převodem časoprostoru diskrétního [PT] do perspektivního [s2]. (věta 1)
Lineární čas newtonovský či relativistický [s] - je odmocnina z počtu pulsů [PT = s2], které hmota nevyužila k pohybu. (věta 2)
Diskrétnímu času PT nenacházím fyzikální význam; kromě
předstihu jednoho děje před jiným. Má tedy odlišnou důležitost
oproti zavedené veličině času v sekundách.
13.2. Přítomnost (obr. 14)
13.3. Současnost
Současnost ve spojitém časoprostoru je určená čtvrtkružnicí (obr. 18.). Patří všem objektům, které na ní leží. Posunované do další posice společným Zdrojovým pulsem PE. Je v ní člověk na Zemi, stejně tak jako kosmonaut v podsvětelné rychlosti; aktuálně může být v PL – kdy jeho tělo nepracuje.
Současnost všech objektů zavedeného časoprostoru podmiňuje jeho rostoucí bodová úsečka. (věta 4)
13.4. Mion
Mion vzniká vysoko v ovzduší Země. Jeho životnost před rozpadem je krátká. Této životnosti [s] mionu by odpovídal dolet jen 600 metrů, a pak se má rozpadnout na elektron a neutrina. Avšak ve skutečnosti letí mnoho kilometrů a i dopadne na povrch Země.
Informatický výklad. Mion střídá svou existenci v pulsech pohybových PL a časových PT:
• PL - mion přeskočí do sousední posice a tehdy se nemění rozložení mnoha bodů, jimiž je tvořen - nestárne. Nezměněný se blíží k povrchu Země.
• PT – Mion zastaví přibližování Zemi. Kdyby měl vnitřní hodiny, jen v těchto PT by mu nabíhal čas, měnil by se. V určitém počtu pulsů Zdroje PE má méně PT, než patří mionu na Zemi.
Mionu, který je na Zemi, se všechny PE mění na PT a tím jsou
k dispozici na změny PL, tedy na rozpad mionu. Dají mionu
kratší život.
13.5. Kruhový pohyb
Informatické vysvětlení, ohledně točení objektu, nemění rozložení jeho bodů - žádné drcení vnitřku.
• Okrajová hmota, ve větší obvodové rychlosti, promění dodávané PE na málo PT a mnoho pohybových PL – pro krouživý pohyb. Proto stárne pomaleji než vnitřní hmota.
• Vevnitř, při menší rychlosti, vznikne mnoho PT a
málo PL. Časové pulsy PT – v okamžicích bez rotace - jsou
tak k využití například ke korozi, která si je mění na PL.
14. Shrnutí
Svět (aktuálně vnímané zážitky) získáváme do vědomí skrz Informatiku. V souvislosti s tím je umožněn současný výskyt mnoha vesmírů, jež si vzájemně nepřekážejí. Jiné bytosti by mohly dostávat zážitky jiného vesmíru.
V těchto jednoduchých mechanických modelech gravitace nezakřivuje časoprostor, nýbrž zakřivuje trasu tělesa v rastru časoprostoru.
Nenacházím nějakou výpočetní výhodu perspektivy s diskrétním prostorem. Popisují promyšlené sestrojení a chod Vesmíru.
Nepředstavuji si vznik Vesmíru zázrakem. Nýbrž vše vysvětluji logickými postupy – počty. Jak by mohla být vytvořená hmota, když by Stvořitelská civilizace žádnou dosud neměla? Zázrakem? Ty chápu až ve vytvořeném prostoru s hmotou a časem, bod za bodem.
Nabízím jen nejjednodušší návrhy, které motivuji Speciální teorií relativity. Tato práce může ponoukat k hlubšímu vysvětlování fyzikálních otázek, založených na mechanických modelech.
Vesmír připodobňuji technickému výrobku.
15. Možný přínos zde představeného mechanického modelu
1. nachází … souměrný diagram času a prostoru, inspirovaný Minkowským
2. zbavuje … rychlost světla postavení postulátu a to zavedením Zdroje pulsací
3. nabízí … nejjednodušší konstrukci a definici veličiny času v diskrétním časoprostoru a zdůvodňuje Lorentzovy transformace
4. převádí … diskrétní časoprostor na spojitý
5. nabízí … současnost. Ač kosmonaut žije ve zpomaleném čase, stále je v současnosti s člověkem v pomalé soustavě, i když ten zestárne dřív než kosmonaut
6. nabízí … časoprostor (Vesmír) v kvantovém provedení, jež nebrání jiným libovolně rozměrným časoprostorům (vesmírům) v jejich existenci
Vesmír je matematizovatelný, což ještě neprokazuje, zda byl
či nebyl promyšleně stvořený. Ale Vesmír je
technizovatelný. Je za ním tvořivá Civilizace. Vysvětluji
Vesmír s časovou základnou, jakou mají elektronické přístroje.
16. Zdroje
[1] Dopis Rudolfa Zahradníka 27. 2. 2008
[2] Výkladový slovník fyziky pro základní VŠ kurz – Mechlová, Košťál za kol. Nakl. Prometheus, Praha 2001, s.192
9. 1. 2025 Úprava