~ Přírodovědní poznání pokračuje úspěšné stále dál. Vychází z tradičních základů, o nichž se stěží pochybuje [1]. ~

~ Přesto se nabízejí alternativy [2]. Ať je Vesmír ve všem kvantovaný, a předávaný rovnou do vědomí. Pak mizí nepřesnosti iracionálních hodnot. Sice je zvládáme přibližným zaokrouhlením, jenže vědě by slušela absolutní přesnost! ~

~ Iracionální zlatý řez se transformuje v racionální. ~

~ Objeví se příčina zpomalení času při pohybu, kterou vyčíslují Lorentzovy transformace ve speciální teorii relativity. ~

~ Konkrétními pomůckami jsou – náhrada Euklidova prostoru perspektivním a - podložení rychlosti světla pulsací. ~

OBSAH ~ názvy kapitol:

1. Světové prostory k Pythagorově větě
2. Speciální teorie relativity – grafy různých časoprostorů. Čas
3. Zlatý řez
4. Vyhodnocení souvislostí

Celkem 16 grafů

~       ~       ~       ~       ~       ~       ~       ~       ~      

OBSAH podkapitol 1. kapitoly

*   *   *

1.1. Euklidův prostor

1.1.1. Geometrické řešení

Prostor je vybavený čtvercovou sítí, proto je všech devět trojúhelníků stejné velikosti (obr. 1). Součet obsahů trojúhelníků označených 1, 2, 3 a 4 je roven obdobnému součtu trojúhelníků 1‘, 2‘, 3‘ a 4‘. Věta a² + a² = u² zde, v geometrii, prokazuje svou platnost.

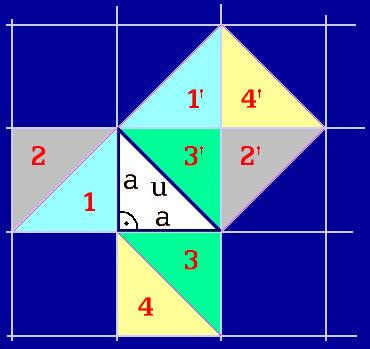
Obr. 1. Pythagorova věta uplatněná ve čtvercové síti

1.1.2. Matematické řešení

I. Příklad

Zadám čtverci racionální stranu a (to jsou čísla např. 10,08 nebo ½) (obr. 2.a). Pak úhlopříčka u vychází vždy iracionální (např. √3).

Zadám úhlopříčku racionální délky u (obr. 2.b). Pak strana čtverce a vychází vždy iracionální.

Následně: není vlastností čtverce, že by jeho úhlopříčka byla zásadně iracionální délky.

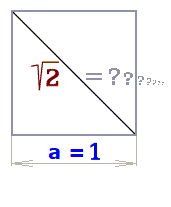
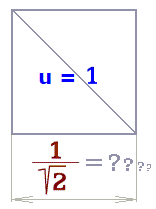Obr. 2.a Čtverec a=1         Obr. 2.b Čtverec u=1

Obojaký výsledek výpočtů obou délek čtverce nabízí, že Euklidova geometrie je sice platná, jenže nepopisuje náš svět. Vždyť některé výpočty jsou bezvýsledné, ačkoliv s jiným zadáním je tatáž délka racionální.

Matematika zaručuje, že výpočet iracionálního čísla nikdy neskončí racionalitou.

1.2. Perspektivní prostor

Náhradu hledám v základnějším zdroji informací – ve zrakovém smyslu. Optika stěží kde sleduje geometrii zrakového zážitku. Nikolaj Ivanovič Lobačevskij: „Závislost sil na vzdálenosti lze zjistit experimenty, ale závislost geometrických vztahů na vzdálenosti lze jen předpokládat.“ [3]

Další prostor na řadě, před Euklidovým prostorem, je perspektiva. Vyzkouším, zda světový prostor je snad primárně určený zrakovým vnímáním.

    Řešení (obr. 3)
Perspektivnímu prostoru zvolím kvadraticky cejchované osy (obr. 3). Řadu přirozených čísel kartézského prostoru, na osách, umocňuji na druhou. Dodržím kladné a záporné poloosy oddělené nulou.

Obr. 3. Převod lineárního měřítka v kvadratické

1.2.1. Porovnání prostoru Euklidova s perspektivním

Přechodem z lineárních na kvadraticky rozmístěné souřadnice (obr. 3) se objekty v prostoru nezmění (obr. 4). Kdežto změní se rovnice a číselný popis jejich velikosti. Kvadratická rovnice Pythagorovy věty se transformuje na lineární:    a + b = c

Lineární rovnice nepoužívají iracionální čísla; s jejich vždy nepřesnou velikostí.

Obr. 4. Kružnice v prostorech Euklidově a perspektivním

1.2.2. Perspektiva omezí výjimky

Posuzuji výsledek v prostoru Euklidově [x, y] a nebo ve zde zobrazené perspektivě [x², y²] (obr. 5).

V Euklidově prostoru, s lineárním cejchováním os, by kružnici velikosti r_Pe=4 patřil poloměr r_Eu=2. Zadanému bodu x_A=1 by vycházela souřadnice iracionální y_A-Eu=√3 a nikoliv racionální y_A-Pe=3.

Obr. 5. Kružnice poloměru r_Pe= 4 v perspektivním prostoru s bodem A [x_A, y_A]

Occamova břitva doporučuje omezit počet výjimek – zde jí jsou iracionality. Lépe obhajitelná je lineární rovnice s racionálním výsledkem. Náš svět popisuje přesněji zrakový smysl - perspektivní vnímání. A to oproti názoru na rozložení hmoty v Euklidově prostoru.

1.3. Převod bodů z diskrétního do perspektivního prostoru

Každému bodu v diskrétním (bodovém) prostoru (šachovnici) lze najít v perspektivním prostoru bod se stejnými souřadnicemi a vzdáleností od počátku (obr. 6).

Například bodům C [2, 3] v obou grafech patří i stejná vzdálenost od počátku, to je 5. V diskrétním prostoru je vždy počítaná na pravoúhlé kroky.

Toto uskladnění bodů v pravoúhlé síti připomíná paměť počítače. Jednotlivá čísla, žádný spojitý záznam.

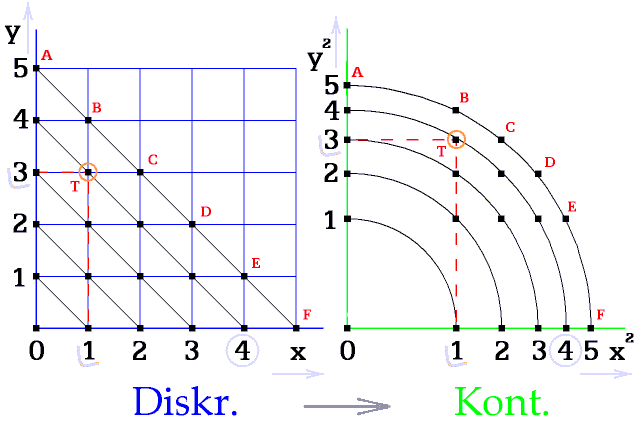
Obr. 6. Převod obsahu diskrétní databáze do perspektivy

1.4. Zhodnocení

Nabízí se, že všechny údaje o světě jsou uskladněné v diskrétní databázi a každý tvor dostává do svého zrakového vnímání jejich perspektivní zpracování. Počátkem souřadnic je mu to místo, kde se právě tělesně nachází. Vzdálenostem mezi body v perspektivě uvažuji Planckovu délku, přibližně 10^-34 m.

Posice ať jsou zaplňovány hypotetickými nejmenšími informatickými body, anebo jsou prázdné. Body pak tvoří hmotu – látku a pole.

Nesoulad s iracionalitami. Geometrická vzdálenost je vždy konečná, ale nekončící výpočet ji nevystihuje. Délka je v matematice racionální nebo iracionální, kdežto v geometrii perspektivního prostoru vždy racionální. Rozpor!

Euklidův prostor není popisem našeho světa.

*   *   *

OBSAH podkapitol 2. kapitoly

*   *   *

2.1. Zpomalování času při pohybu ve spojitém časoprostoru

CITACE: Einsteinovská kontrakce byla odvozena pouze užitím základních postulátů teorie relativity a nemůže být proto vyložena pomocí třeba atomární teorie hmoty. Je třeba ji chápat jako cosi, co je zcela prvotním jevem a co již nelze vysvětlit pomocí jednodušších jevů - Jan Horský. [4]

Podle Lorentzových transformací se zpomaluje čas při každém pohybu; teoretický poznatek byl měřením ověřen jako skutečný. Věda nenachází ve spojitém časoprostoru zdůvodnění - vznikl postulát.

Jinak v diskrétním časoprostoru, který navíc vybavuji generátorem pulsů. Tento diskrétní časoprostor není přímo přístupný lidským smyslům.

Pulsy časové základny ať podkládají jak čas, tak pohyb – k nejstručnější nabídce k našemu světu [5].

V diskrétní databázi má posice, určená pro uskladnění informatického bodu, obsah 1 bit. Tím je určena i velikost tohoto bodu.

Diskrétní časoprostor nepřevádím do hypotetického Euklidova prostoru, nýbrž rovnou do perspektivy, kterou vnímají lidské smysly.

2.2. Grafy

2.2.1. Minkowského graf

Po vzniku teorie relativity bylo potřebné zdůraznit nový poznatek o omezené rychlosti pohybu (obr. 7). Hmota v soustavě vyšla z počátku času [t] a prostoru [l]. Může se pohybovat výhradně ve žluté ploše, prokázala teorie.

*… foton (částice světla)
Obr. 7. Minkowského graf

2.2.2. Souměrný graf v Euklidově časoprostoru

Teorie relativity vyhlásila rovnocennost času a délky. Tu ukazuje zcela opomíjený souměrný graf (obr. 8). Svislá osa slouží času a vodorovná délce dráhy. Zvedání vodorovné polopřímky Minkowského grafu je zde nahrazeno rostoucím průměrem časoprostorové kružnice.

Navrhnutí časoprostorové Euklidovské kružnice:

Speciální teorie relativity současnost neuvažuje. Naopak v této informatické teorii čtvrtkružnice souměrného časoprostoru ukazuje současnost objektů, jež na ní leží.

Ať Země je bez pohybu, kdy postava na ní má čas t=3 s, kdežto ostatní objekty, jež také vyšly ze společného počátku souřadnic, mají vlastní čas pomalejší (obr. 8). Kosmoplán, v pozemském čase 3 s, má vlastní čas 2,8 s, když odlétl od počátku 300.000 km.

Souměrný graf umožňuje smyslově posoudit zpomalování času.

2.2.3. Souměrný graf v diskrétním časoprostoru

Uvážím využití 20 generovaných pulsů PE hypotetického vesmírného zdroje (obr. 9). Předpokládám 1 PE (puls Zdroje) pro jednotku Planckova času nebo délky.

z… pulsy zdroje PE
z_t… pulsy časové PT
z_l… pulsy délkové PL

Stojící postava využívá všechny PE jako časové z_t [PT]. Foton na vodorovné ose všech 20 PE mění v pohyb z₁ = 20 PL. Kosmoplán letí poloviční rychlostí světla (diskrétního prostoru). Střídá využití pulsů délkových PL a časových PT, celkem 20 PE.

2.2.4. Souměrný graf v perspektivním časoprostoru

Naše zrakové pozorování okolí vnímá délkovou perspektivu. Zde zkouším vlastnosti souměrného perspektivního časoprostoru (obr. 10), s objekty vybavenými počtem zdrojových pulsů z = 20 PE.

K tomu spekuluji o čase, jako veličině rovněž podléhající perspektivě. Tento názor je podporován skutečností časové přítomnosti, ze které se nedovedeme vyvázat. Její příčinou může být nejdelší časový úsek 0-1 na svislé ose. Však Albert Einstein kdysi uvažoval, že k našemu přesvědčení o určitém umístění v čase není fyzikální důvod. To bylo ve spojitém lineárním časoprostoru.

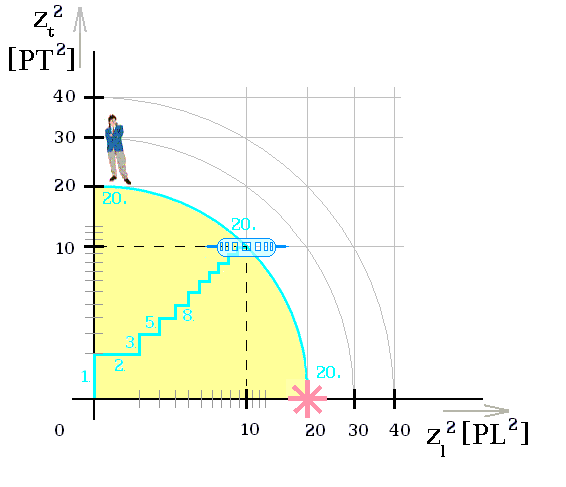
Obr. 10. Souměrný graf diskrétního časoprostoru

2.2.5. Převod časoprostoru perspektivního do Euklidova

Používáme Euklidův časoprostor. Převod do něj sleduje tato kapitola 2.2.5. a to z diskrétního a z perspektivního časoprostoru. Obrázky nezohledňují Planckovy konstanty vůči času a délce, vůči PT a PL.

Obr. 11. Diskrétní časoprostor                       Obr. 12. Minkowského a perspektivní časoprostor

Obrázek 11. ukazuje, jak se všechny objekty vzdalují od svého společného počátku časoprostoru. Modrá šikmá úsečka pro z = 40 PE by, lépe, měla být nahrazená 40 oddělenými body, jak by se patřilo v diskrétním časoprostoru (obr. 11).

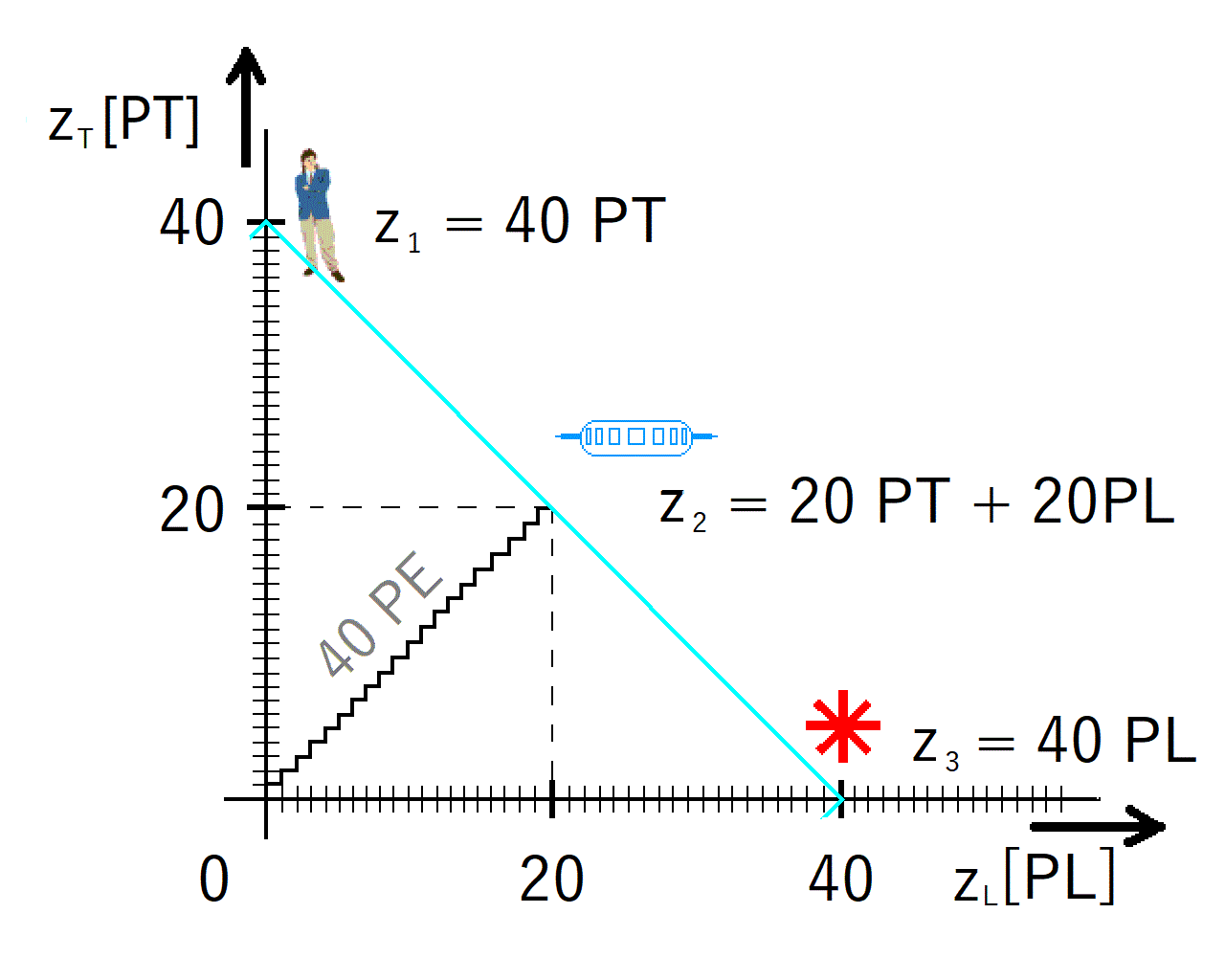
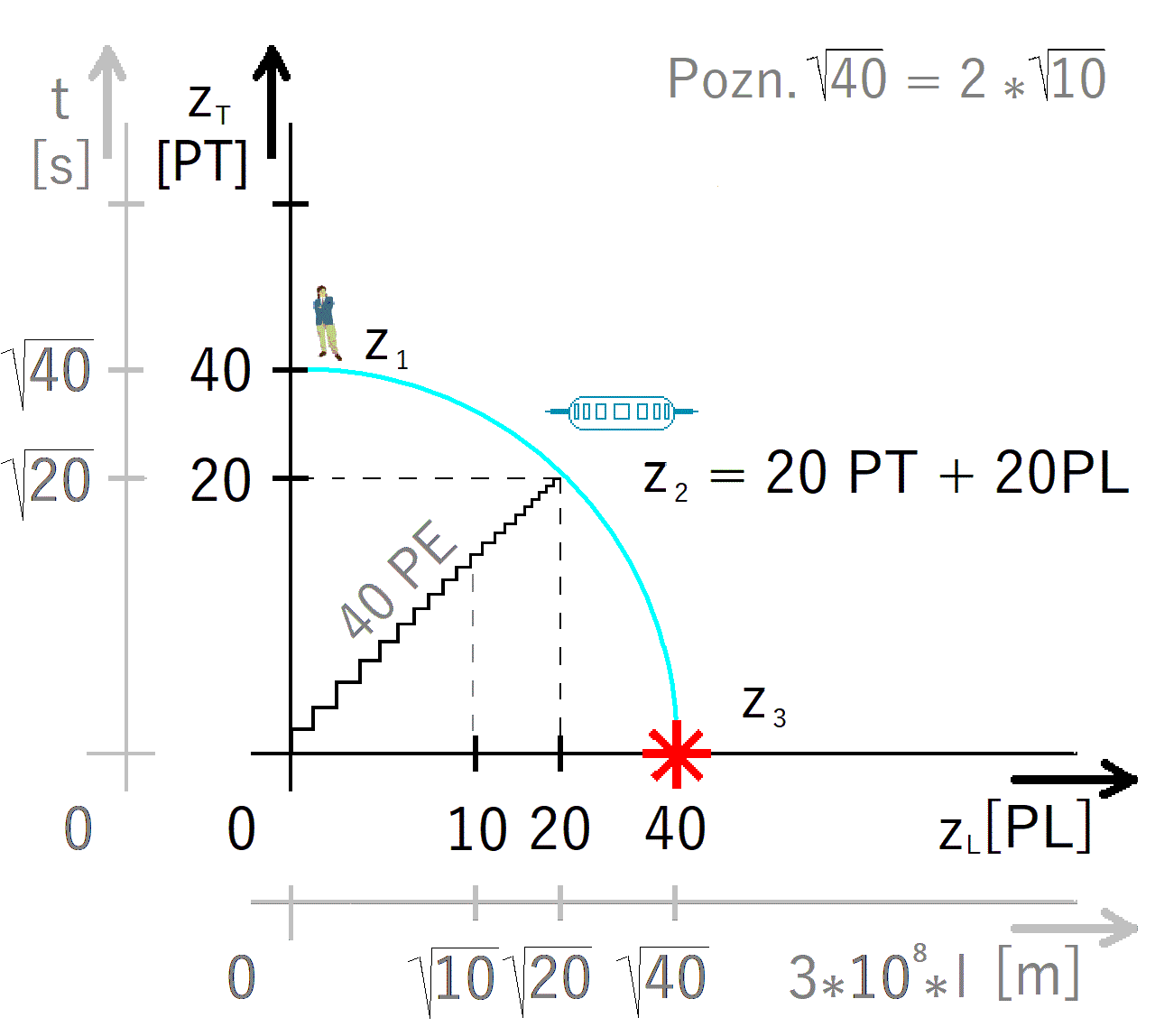
Obrázek 12. užívá dvoje měřítka. Přímo na osách grafu z_T a z_L je cejchování nelineární - pro perspektivní časoprostor.

Cejchování os lineárního Euklidovského časoprostoru: t [s], l·3·10⁸ [m].

Perspektivní časoprostor se vyvaruje iracionalit. Například 40 PT postavy v perspektivním časoprostoru značí v obvyklém Euklidovském t = √40 s. Kosmoplán využije 40 PE na dva účely: na čas a na dráhu. Diskrétní čas z_T = 20 PT pro √20 sekund v Euklidovském prostoru. Podobně délka z_L = 20 PL vytvoří Euklidovskou délku √20·3·10⁸ m.

2.2.6. Definice diskrétního a newtonovo - einsteinovského času

Tyto úvahy nabízejí - kvantita času souvisí s počtem nevyužitých pulsů zdroje PE. Čas podmiňují pulsy PT – kdy bod hmoty se neposunul do sousední posice.

Čas určují ty pulsy, které nebyly body hmoty nijak využity. Nevyužité pulsy čas stanovují, ovšem časem nejsou. Časem je nazvu až po kvadratickém přepočtu ve prospěch perspektivního vnímání. Viz svislá osa (obr. 12).

Dál lze uvažovat návaznost s obecnou TR, kde gravitace také zpomaluje chod času.

Čas určují ty pulsy, které nebyly body hmoty nijak využity.

II. Příklad (fázovaný obr. 13)

Obr. 13.a Přejděte na 13.b

Popíšu chování tří korábů

▪ Horní koráb nevyletěl, takže všechny poskytnuté zdrojové pulsy PE se mění na časové PT. Lidé v něm stárnou nejrychleji.

▪ Prostřední koráb přeskočí při každém druhém pulsu.

▪ Spodní koráb má skoro rychlost světla; zastaví se na trvání 1 pulsu až po mnoha pohybových pulsech.

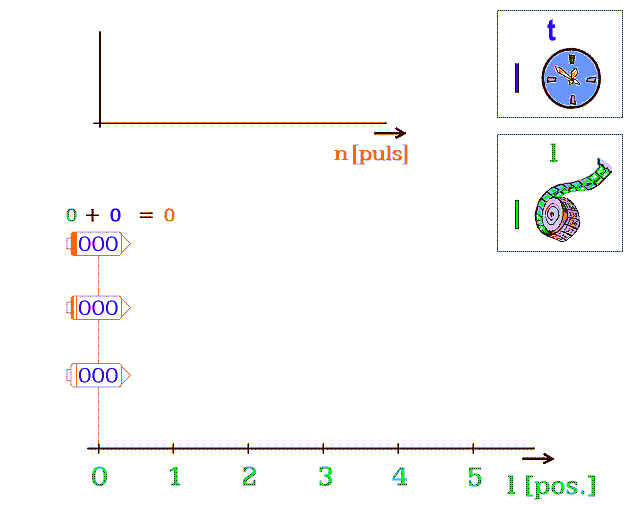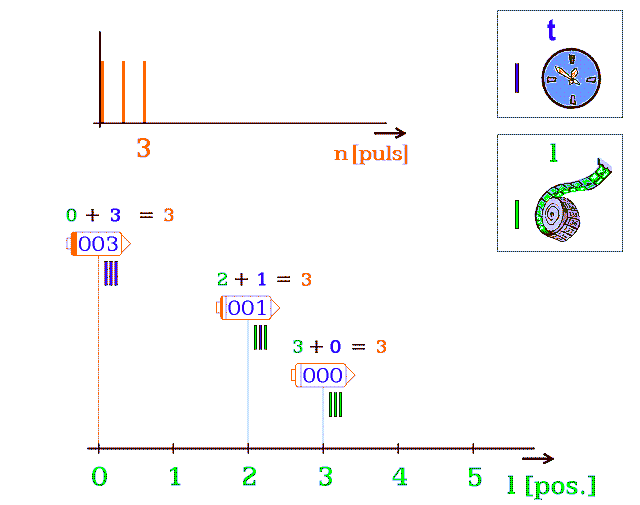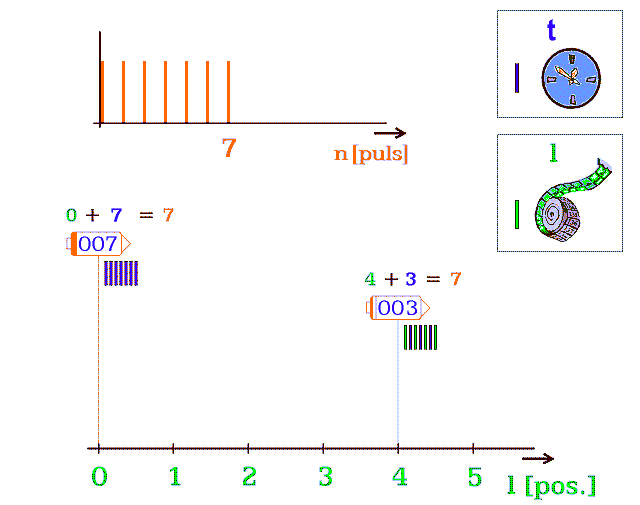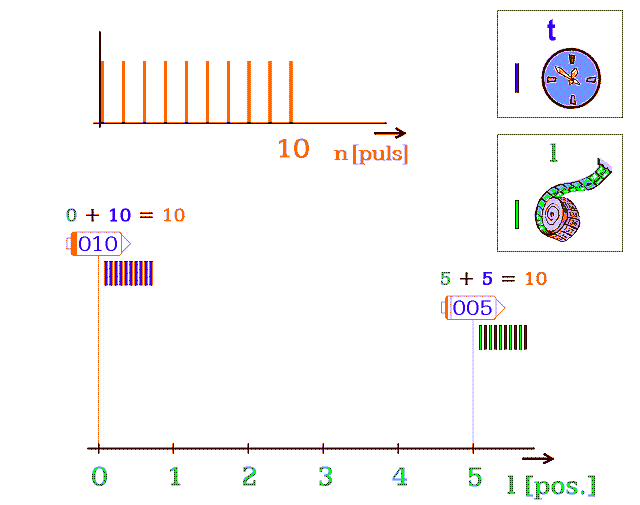
Obr. 13.b Tři vesmírné koráby v různých rychlostech pohybu. Čísla v korábech značí jejich diskrétní „čas“ - počet pulsů nevyužitých k translaci. Součet dvou čísel, nad korábem, počítá dosud proběhlé pulsy. Diskrétní „čas“ v pulsech není časem v sekundách

Zvolené postupy nabízejí zdůvodnit zpomalení času při pohybu. Zásadní je nečekaný generátor pulsů, jenž podkládá Vesmír.

*   *   *

OBSAH podkapitol 3. kapitoly

*   *   *

3.1. Zlatý řez v Euklidově prostoru

Zlatý řez vyjadřuje mimořádný poměr dvou stran obdélníka (obr. 14., 15.). Jeho význam našla i sama exaktní matematika a to v oboru Fibonacciho čísel.

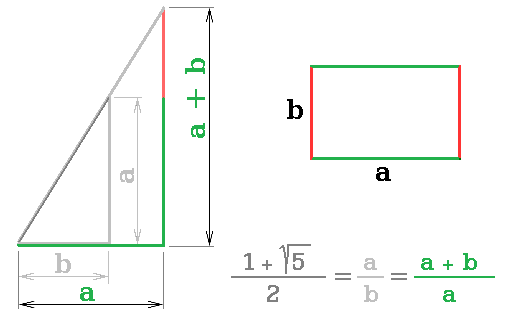
Obr. 15. Podobné trojúhelníky. Obdélník zlatého řezu. Výpočetní poměr zlatého řezu.

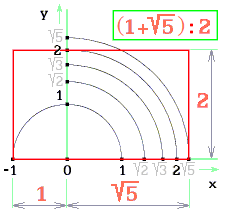
Obr. 14. Model zlatého řezu v Euklidově prostoru má poměr (1+√5)/2

Platí: a/b = (1 + √5)/2

Podíl je iracionální: 1,6180339887498…

3.2. Zlatý řez v perspektivním prostoru

Geometrie perspektivy změní matematický poměr. Strany obdélníka euklidovského prostoru a = 1 + √5, b = 2 budou přepočteny.

Souřadnice [x, y] bodů [-|1|, 0], [√5, 0], [0, 2] (obr. 14) umocním na druhou. Nové souřadnice [-(|1|²), 0], [5, 0], [0, 4] určují obdélník v perspektivním prostoru (obr. 16.)

Obr. 16. Zlatý řez v perspektivním prostoru

• Délku √5 nahradí délka 5.
• Svislou délku strany b = 2 nahradí délka 4.
• Jednotková délka se převádí beze změny – na vodorovné ose od 0 až k -1.

Perspektivní matematika vyjádřila délky stran bez zaokrouhlení – přesně. Vznikl obdélník o stranách a = 6, b = 4. Příčinou odlišného údaje o délkách je jiný průběh cejchování os, jiná geometrie.

Zlatý řez nabízí užít Occamovu břitvu, která podpoří právě racionální poměr 3:2. Upřednostní svět vytvořený našimi zážitky a nikoliv starověkým Euklidovým prostorem. Nikoliv euklidovských nepřesných 1,618…, nýbrž ve zrakovém prostoru 3:2. Racionální poměr 3:2 je o to závažnější, když je tvořen dvěma velmi malými přirozenými čísly.

*   *   *

OBSAH podkapitol 4. kapitoly

*   *   *

4.1. Svět tvořený zážitky

Tato modelová práce odmítá Euklidův prostor jako popis světa, podobně lze nahlížet i na další prostory s iracionalitami.

Výhrada - otázkou je, zda iracionality vyhovující v matematice, jsou výstižné i pro náš vnímaný svět, pro fyziku. Technickým konstrukcím vyhovují zaokrouhlení ve výpočtech. Kdežto pro vědu – fyziku - iracionality připomínají něco nehotového. Vždyť úsečku konečné délky - vyjadřuje nekončící výpočet.

Informace o světě získává člověk svými smysly. Již Ernst Mach upozorňoval, že nezkoumáme hmotu, ale zážitky hmoty [6]. Perspektivní zrakový prostor, jenž patří našemu vnímání, považuji za nevyvratitelný. Obsahuje výhradně racionální čísla. Nepotřebuje zavádět nová čísla - iracionální – viz S. Stevin *1548. Ač naší civilizaci jsou dosud velmi potřebná a prospěšná.

Zde zveřejněný způsob popisuje promyšlenou konstrukci Vesmíru, aniž by vytlačil výpočty v dosud zavedeném Euklidově prostoru.

Výhrada - smysly jsou ošidné. Ovšem ta ošidnost spočívá až v přijímači – v oku. Kdežto vysílač zrakových údajů může být naprosto přesný. Systém, který přepočítává údaje z diskrétního prostoru do perspektivního. Aniž bych mohl popsat konstrukci tvora – jakým postupem je napojený na zdroj informací.

Naše vjemy nám představují svět, jenž není podložený hmotou. Svět tvořený informatikou.

Svět tvořený zážitky, bez hmoty, vystihuje   virtuální realita

4.2. Časová základna podkládá náš svět

Zpomalování času při pohybu vysvětluje teprve zavedení pulsací, jež ovládají každý informatický bod hmoty. Viz 2. kapitola.

Vesmír, podložený generátorem pulsů, poukazuje na mimořádně pokročilou stvořitelskou civilizaci za našim světem

LITERATURA

[1] Jiří Mrázek a kol.: Kde začíná budoucnost. Naše vojsko, Praha 1989, s.366

Na druhé straně se však dnes stále více ukazuje i to, že v myšlence kontinua je nějaká záhada, začínající budit dojem něčeho nezdravého. Prostě kontinuum začíná budit nedůvěru odborníků. Tito odborníci začínají volat po revizi všeho, co s kontinuem souvisí. Chtějí nahradit kontinuum něčím nespojitým, chtějí kvantovat matematiku nějak podobně, jako již předtím začali fyzikové kvantovat fyziku. Ozývají se další a další hlasy, požadující znovuprověření všeho, co bylo vybudováno na pojmu nekonečně malé veličiny, byť by to byly mat. vzorce a metody nesčetněkrát prověřené praxí. Tito odborníci ukázali, že lze stejné vzorce odvodit i z představ "kvantované" matematiky, pracující nikoli s veličinami nekonečně malými, nýbrž velmi malými.

[2] Vorovka, Karel: Kantova filosofie ve svých vztazích k vědám exaktním. JČMF, Praha 1924

Avšak Riemann byl také prvý, kdož se zabýval myšlenkou prostoru, jehož zakřivení a tedy metrika by se od místa k místu měnily. --- prostor takového druhu jako ideální útvar myšlenkový je logicky možný. s.64

Ve své práci z roku 1868 hleděl Helmholtz dokázati, že axiomy geometrie jsou aposteriorního původu a že euklidovský způsob názoru na prostor není pro nás žádnou nutností. Za tím účelem užil Bertramiova zobrazení celého prostoru pseudosférického uvnitř konečné koule prostoru euklidovského, při němž přímce odpovídá přímka a rovině rovina, současně však rozměrů od středu k povrchu koule dle jistého zákona ubývá. Helmholtz si nyní myslí uvnitř této koule pozorovatele, jehož tělo i nástroje by podléhaly témuž zákonu. Takový pozorovatel by měl počitky a vněmy odpovídající prostoru pseudosférickému, počitky to, které si dovedeme popsati a tedy i představiti, dle mínění Helmholtzova je tudíž zjevno, že bychom při takové jiné zkušenosti dospěli také k  jinému názoru na prostor. s.66

Diskontinuitní představy o prostoru hájili Giordano Bruno a T. Hobbes, kteří oba tímto atomistickým nazíráním na prostor dostali se do odporu k matematice, popírajíce oprávněnost čísel irracionálních a pravdivost věty Pythagorovy. s.91

R. Dedekind: Má-li prostor vůbec reálnou existenci, nemusí ještě proto býti spojitým, nespočetné jeho vlastnosti zůstaly by týmiž, i kdyby byl přetržitým." s.93

[3] B. G. Kuzněcov: Vývin názorov na svet. Osveta, Bratislava 1962, s.251

[4] Horský, Jan: Speciální teorie relativity. UJEP Brno, SPN 1972, s.24

[5] A. P. Juškevič: Dějiny matematiky ve středověku. Academia, Praha 1977

V arabské filosofické literatuře se projevilo atomistické učení o prostoru a času, které jak známo zavrhoval Aristoteles a v matematické formě Eudoxos a jejich stoupenci. Toto hledisko zastával a rozvíjel Abu ´l-Hasan Alií ibn Isamá´íl al-Ašarí. Na základě učení o diskrétním charakteru času a pohybu, mutakallimisté dělali neodůvodněný indeterministický závěr, že v každém právě probíhajícím atomu času Alláh vždy znovu tvoří celý svět a tedy ve světě nemohou existovat žádné příčinné souvislosti.

Toto učení nezůstalo bez odezvy ani v matematice. Z hlediska mutakallimistů jsou dvě libovolné veličiny stejného druhu vždy souměřitelné a neexistují tedy iracionálně. Při rozpracování své obecné teorie proporcí se Chajjám o tomto pojetí zmiňuje a ačkoli ho nesdílí, nezavrhuje možnost vítězství matematického atomismu v budoucnosti a snad ani nepovažuje za vhodné ji zavrhnout. s.290

[6] Dratvová, Božena: Positivismus ve fyzice. JČMF 1924

Mach je přesvědčen, že zvláště fyzika získá největších vysvětlení od biologie, a sice od analysy smyslových počitků. Předměty vnějšího světa nezpůsobují počitků, nýbrž komplexy počitků tvoří tělesa.