
V teorii relativity je již po celé století známý Minkowského diagram. Ukazuje propojení času a prostoru; zavádí časoprostor. Newtonovský přístup jinak; uznával vzájemnou nezávislost prostoru a času.
Obě veličiny se vyskytují společně, pod jedním vlivem. Přitom čas, jako čtvrtý rozměr světa, chápeme v propojení se třemi délkovými rozměry odlišným způsobem. Přesto jej posuzuji jako čtvrtý geometrický světový rozměr.
Časoprostor působí ve světě tím způsobem, že neustále určuje buď nárůst času, anebo pohyb v geometrickém prostoru. Extrémními případy jsou foton - jemu čas nepřibývá, kdežto objektu bez pohybu čas přibývá nejrychleji.
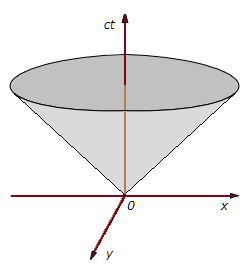
Ve dvojrozměrném prostoru lze časoprostor znázorňovat následovně (obr. 1). Postup objektu časem, podle svislé osy - a pohyb prostorem, podle vodorovné. Respektováním mezní rychlosti světla vznikne kužel, jehož objem je určující objektům, jež vyšly z počátku 0. Není jim dovoleno stoupat mimo kužel; to by značilo překročení rychlosti světla. Kužel se stále zvětšuje, tak jak tmavošedá rovina postupuje nahoru v čase.
Osy vodorovná a svislá jsou cejchované toutéž jednotkou. Užití ct pro svislou osu, namísto t, dovoluje společnou jednotku - metry, oběma osám časoprostoru. Ve výpočtu, pro svislou osu, se sekundy krátí: 1 m/s · 1 s = 1 m.
Geometrickému 1D prostoru se nezobrazí kužel, ale jen trojúhelník (obr. 2). Zde rovnoramenný, zásluhou měřítek dílků 1 s ~ 300.000 km. Opět se hmota nemůže objevit mimo vybarvenou plochu. Obrázek určuje kosmoplánu rychlost 300.000 km za 3 sekundy.
Diagram však názorně nezobrazí rovnocennost času a prostoru. Hodnotí stav, který patří nehybné postavě. Jenže fotonu čas nenabývá, měl by se pohybovat po vodorovné ose.
Uplatňuji odlišný graf, který však dosud bývá mimo zájem fyzikální teorie (obr. 3). Protože čas a pohyb prostorem jsou v časoprostoru rovnocenné, lze obdobně užít obě osy. Svislá - pro čas a vodorovná - pro dráhu. V ocejchování grafu sjednotím dílky délkově: 1 sekunda - svisle a 300.000 km - vodorovně.
V Minkowského diagramu se časoprostor projevoval zvedáním kruhu po časové ose - pro 2D geometrický svět. Nebo zvedáním úsečky pro 1D geometrický svět.
Časoprostor v souměrném obrázku určuje neustálý rovnoměrný růst průměru čtvrtkružnice, s jejím středem v počátku časoprostoru.
Objektům v pohybu se relativisticky zpožďuje čas. Což souměrný graf zobrazuje snadno.
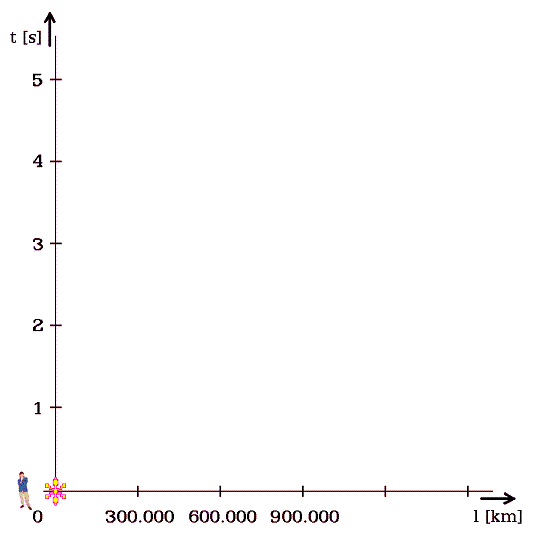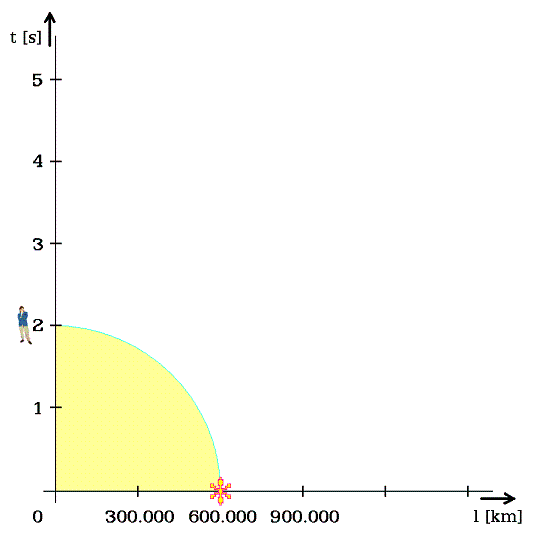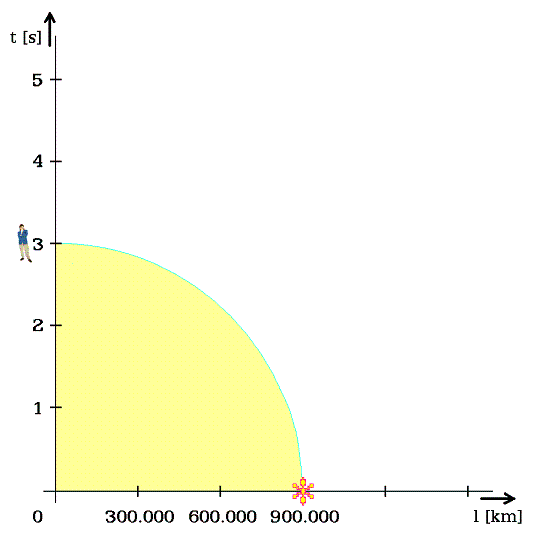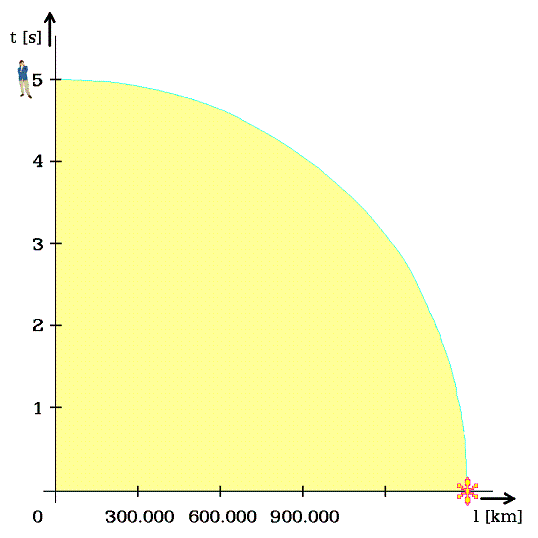
Například kosmoplán ať má rychlost 300.000 km za 3 sekundy pozemské. Na svislé ose lze odečítat jeho zpomalený čas (obr. 4). Třem sekundám pozemským odpovídá čas na kosmoplánu jen 2,8 sekundy. Kosmonauti stárnou pomaleji.
Graf umožňuje nalézt vlastní (zpomalený) čas orientačně, snadným vyhledáním na vodorovné a svislé ose. Určující je přitom umístění sledovaného kosmoplánu na obvodě čtvrtkružnice. Podle jeho rychlosti na odpovídajícím místě jejího obvodu.
Například ať má rychlost 750.000 km/3 sekundy. Pak z vodorovné osy nutno vztyčit kolmici v bodě 750.000 km, a z průsečíku s obloukem najít ve vodorovném směru zpomalený relativistický čas, který odpovídá zadané rychlosti (250.000 km/s).
Naše stará Apolla a Sojuzy mívají rychlost tak asi 30 km za 3 sekundy, takže za 3 sekundy pozemské na nich uplyne čas přibližně také 3 s. Podrobnosti o nepatrném zpoždění času z grafu neodečteme.
|
v |
l |
tP |
tM |
|
km/s |
km |
s |
s |
|
100.000 |
300.000 |
2,82 |
2,8 |
|
200.000 |
600.000 |
2,28 |
2,2 |
|
250.000 |
750.000 |
1,65 |
1,6 |
v … rychlost objektu
l … dráha objektu uražená za 3 sekundy
tP … vlastní čas objektu - počítaný
tM … vlastní čas objektu - měřený na svislé ose 4. obrázku
Výsledky z tabulky ukazují, že grafický princip pro zjištění relativistického času přijatelně posloužil. Využití souměrného diagramu může studentům pomoci při pochopení problematiky speciální teorie relativity. Přesné výsledky však poskytnou relativistické výpočty.