Fibonacciho čísla v perspektivě   💾  

Ital Fibonacci v 13. století určil číselnou řadu, která se svou podstatou neodlišuje od zlatého řezu. V dalším sleduji, zda také Fibonacciho řada podporuje důležitost perspektivního zrakového vjemu - pro možný výklad existence vnímaného světa.

OBSAH

1. Fibonacciho řada

Jeho řada začíná čísly  1, 1, 2, 3, 5, 8, 13, …

Fibonacciho řada pokračuje vždy dalším sčítáním posledních, tedy největších dvou čísel dosavadní řady. Začíná se číslem 1, pokračuje se znovu 1, ale pak už řada pokračuje obhajitelněji:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …

1.1. Řešení začátku Fibonacciho řady

Lze obhájit začátek řady jinak; od nuly.

Má-li řada pokračovat sčítáním dvou předchozích čísel, ať má v začátku nachystaná první dvě čísla bez sčítání (to budou 0 a 1). Třetí číslo, (to bude 1), vznikne sečtením prvních dvou 0+1:

1.2. Ověření k zlatému řezu

Podíl dvou sousedních čísel Fibonacciho řady je, již z definice, racionálním číslem: například 5/3. Velikostí se blíží iracionálnímu číslu zlatého řezu. Používám-li stále větších sousedních čísel, pak se podíl přibližuje zlatému řezu stále víc. Lze posuzovat, zda velké číslo obsahuje víc informací:

1.3. Výpočet zlatého řezu

1.4. Ověření řady dosazením do zlatého poměru

Součtem (a + b), tedy čitatelem na levé straně rovnice, je 21.
Větším číslem  a  je 13.
Menším číslem  b  je 8.

Dosazení do zlatého řezu:  (13 + 8)/13 = 13/8

Fibonacciho řada tedy odpovídá pravidlům výpočtu zlatého řezu. Její sousední čísla se přibližují poměru:  (a + b)/a nebo  a/b. Dosazení do {1} upozorňuje na neplatnost rovnice, v souvislosti s iracionalitami.

1.5. Výpočet ze čtyř sousedních čísel řady

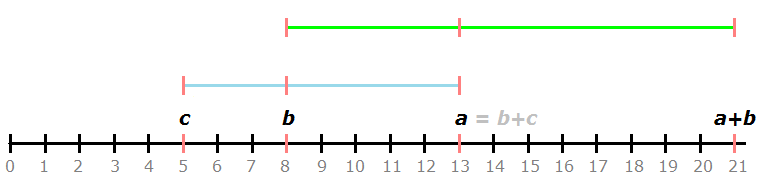
Obr. 1. Dva zlaté řezy. Uvažují čísla  c, b, b+c  a také  b, a, a+b

Pro spojení dvou zlatých řezů zavedu čísla  c, b, a, a+b,  jež vybírám z Fibonacciho řady. První dvojice  b, a  aproximuje zlatý řez; platí  a > b:
(a + b)/a = a/b        {1}

Dále použiju číslo  c < b. I tato dvojice  c, b  aproximuje zlatý řez. (Platí a = b + c):
a/b = b/c                {2}

Dosazením do {1}:
(b² + b)/b² = b²/b    | ·b²
b² + b = b⁴/b
b³ – b² – b = 0        {3}

Zkouška rovnice zlatého řezu:
Dosazením zlatého řezu  b = 1,6180339  ověřím rovnici {3}, která vznikla srovnáním dvou řezů.
b³ =  b² + b            {3}

Dosazením racionálních čísel do {3} nebude rovnice splněna, avšak rozdílem mezi výsledky nalevo a napravo lze posoudit její nepřesnost.

Iracionální číslo zlatého řezu, dosazené do rovnice racionální hodnotou  b = 1,6180339, dává vzniknout - namísto nuly - číslu málo odlišnému, o čtyři desetimiliontiny. Při sledování všech desetinných míst, ve výpočtu, je rozdíl menší: 0,000 000 321 100 105 701 781.

Dávno zpracovaná teorie zlatého řezu jej počítá i z rovnic vyššího řádu, např.:

b⁶ =  b⁵ + b⁴

2. Perspektivní geometrii inspirovat Fibonacciho řadou

Uvažuji perspektivní prostor [x², y²]. V něm zavedu souosé kružnice, jež rostou svým poloměrem, zvětšovaným po 1. Pak každé další mezikruží má vždy stejný obsah jako předchozí (viz obrázek mezikruží). Nacházím, že čísla na perspektivní ose jsou sice nelineárně rozložena, ale zato s velikostmi mezikruží jinak.

Na důležitost obsahu plochy - a nikoliv geometrické délky - zkusím navázat. Zobrazím čísla Fibonacciho řady – a to přepočtené na čtverce. Každému z čísel řady určím být stranou čtverce.

3. Fibonacciho řada na číselné ose perspektivního geometrického prostoru

Ve vědě dovedeme pochválit nalezenou pravidelnost - vládnoucí zákonnost našeho Vesmíru. Zkusím ověřit rozložení Fibonacciho čísel na ose perspektivního prostoru (obr. 2).

Obr. 2. Rozložení deseti Fibonacciho čísel na ose perspektivního prostoru

Jsou to: 1 - 2 - 3 - 5 - 8 - 13 -21 - 34 - 55 - 89

Grafické hodnocení:

Mezi 2-3 je mezera menší (měřeno v milimetrech) než mezi 1-2 nebo mezi 3-5. Toto optické hodnocení ukazuje nepravidelnost. V dalším růstu čísel se mezery pak už zvětšují.

Fibonacciho čísla, rozmístěná na číselné ose, neukazují svým uspořádáním krásnou pravidelnost. A zrak nevnímá a následně nehodnotí matematické pravidlo, kterým jsou rozmístěna.

Protože u Vesmíru, v němž provozujeme svůj život, často sledujeme nejen vzhledovou, ale i sluchovou, čichovou, chuťovou a hmatovou jeho krásu, jeho příjemnost, pak tato sledovaná nepravidelnost nabádá hledat dál - jiným směrem.

4. Příčina propojování Fibonacciho řady s perspektivou

Nahradím číselnou osu, přímku - číselnou plochou, a následně zhodnotím vzniklý řád. 

Ovšem – k čemu číselná plocha?

Může být, že dávný náš předek by na číselné ose nenašel nic zajímavého. Jenže vzdělancům bývá ona rovnoměrně cejchovaná osa, po staletí, relevantním základem kartézských souřadnic.

Podobně zkouším posuzovat, zda plocha perspektivního prostoru hodnotí důležitost perspektivní matematiky, s její kvadraticky cejchovanou číselnou osou - tak jako lineárně cejchovaná číselná osa prospívá Euklidově prostoru.

5. Číselná plocha

Obr. 3. Fibonacciho řadu vyjadřuje číselná plocha

Sestava začíná nejmenším čtverečkem o délce strany 1 (obr. 3). Vedle něho je stejný čtvereček. Nad dvojicí je čtvereček o straně 2, kterou mu vymezují délky stran obou předchozích čtverečků.

Totéž pak nachystá čtverci o straně 3 předchozí dvojice stran: 2 a 1, tak jak jsou Fibonacciho čísla seřazena.

Popsaný způsob bývá užitý k založení spirály, jež z Fibonacciho čísel vychází.

Zde však zdůrazňuji jinou skutečnost - zatímco rozložení Fibonacciho čísel v 1D geometrickém prostoru neukazuje nějaký jejich řád, teprve rozložení ve 2D prostoru, s jejich kvadratickým zpracováním, ukazuje srozumitelný řád. Svým zrakovým smyslem laicky zhodnocuji kvadratické zpracování Fibonacciho čísel, jež zde bylo použité.

6. Co vyplývá z perspektivního prostoru

Fibonacciho řada byla využitá pro zobrazení rostoucích čtverců. Tento známý jev by mohl zdůrazňovat, jak zásadní je našemu žitému světu - perspektivní geometrický prostor [x², y²].

• Nejde tedy jen o zlatý řez, jehož iracionální poměr  (1+ sqrt(5))/2  Euklidovy geometrie se změní - a to v racionální poměr  3/2  perspektivní geometrie.
• Nejde jen o matematické vyjádření velikosti úhlopříčky čtverce, která se tímtéž transformováním prostorů přemění z délky iracionální v racionální.
• Nejde jen o speciální teorii relativity, která zavedením diskrétní a pak perspektivní geometrie sleduje důvod zpomalování času a i jeho definici.


• Nýbrž i téma tohoto textu mírně podporuje možnost docenit perspektivní prostor jako možný základ našeho světa. Včetně diskrétního prostoru, jehož při vysvětlování perspektivy nevynechávám.
  

Přibližování promyšlených souvislostí, jimiž je svět založen, může následně měnit naše smýšlení a tím i chování. Přivést nás k důvodnému přebírání zásad, jakými co nejlépe jednat ve světě. Dopomoci nám k lepším výsledkům našich životů.

Následně fyzikální veličiny v perspektivě ztrácejí své iracionální hodnoty - ve kterých existující veličinu představoval její bezvýsledný výpočet. Kvadratické rovnice se transformují v lineární; iracionality jsou vyloučené. Například pro Pythagorovu větu (obrázek P. v.), rovnici kružnice - tatáž věta (obrázek kružnice v diskrétním a perspektivním prostoru), Newtonův gravitační zákon (obrázek N. g. z.), Lorentzovy transformace (obrázek perspektivního časoprostoru), Einsteinův výpočet energie…

Vědci někdy připomenou krásu matematického zpracování Vesmíru. Zde ji nahlížím v kvadrátu Fibonacciho čísel, v jejich geometrickém vyjádření. Jenže, jestliže věda nemá pochybnosti nad výskytem iracionalit v mnoha svých výpočtech, a vysvětluje Vesmír bezvýslednými výpočty - pak mohla by vůbec uznat důvod krásy u kvadraticky zpracovaných čísel - u čtverců čísel - Fibonacciho řady?