
~ Model nabízí výklad Vesmíru, který je podložený diskrétním (bodovým) prostorem a pulsy časové základny. Z jejích pulsů vzniká jak čas, tak i pohyb *). Čas probírám ve fyzikálním, nikoliv ve filozofickém uchopení.
~ Dokud čas Newtonovy fyziky byl neměnný, pak na něm nebylo co zkoumat. Kdežto závislost relativistického času na rychlosti dovoluje čas popsat, snáze vysvětlit. Když to není pouhý sled rovnoměrně řazených obrazů hmoty.
~ Vybraný model zkouší vyloučit paradoxní zkracování obvodu rotujícího kotouče. Nahrazuje je jiným účinkem na geometrickou délku (kap. 5.1.3.)
~ Diskrétní (bodový) časoprostor zde není převáděný do hypotetického Euklidova prostoru, nýbrž rovnou do perspektivy, kterou vnímají lidské smysly.~ Někdy fyzika odmítá rozlišovat mezi minulostí, budoucností či přítomností. Model nabízí vliv navržené konstrukce času na lidský pocit přítomnosti (kap. 10.2.).
~ Použitý geometrický prostor - vnímaná perspektiva - vylučuje výskyt matematických iracionalit. V souvislosti s tím umožňuje současný výskyt mnoha vesmírů, jež si vzájemně nepřekážejí (kap. 10.3.).
~ Práce uvažuje nové pohledy; převádí diskrétní prostor do smyslových spojitých zážitků, avšak nesleduje relativitu souřadných soustav. Takovou otázku může posoudit další práce v podobném směru, v potřebném hlubším uchopení.Z tohoto hlediska se jeví nedůsledné, že vzdálenosti (intervaly) v prostoročase se v různých směrech měří v různých jednotkách: ve směrech prostorových v metrech, podél časové osy v sekundách. Je to podobné, jako kdybychom zde na zemi vzdálenosti v horizontálním směru (tj. délku a šířku) měřili v metrech, zatímco vzdálenosti ve vertikálním směru (výšku a hloubku) měřili třebas v palcích. Vznikaly by tak zbytečné komplikace při měření délek v "šikmých" směrech - stanovování vzdáleností bodů s odlišnými horizontálními souřadnicemi ležících různě vysoko.
V Einsteinových rovnicích pole zůstávají zachovány fyzikální a geometrické veličiny jako veličiny oddělené. Myšlenkou jednoty fyziky a geometrie navázal Einstein na Riemanna.
Navržený model vyhovuje Ullmannově požadavku. Obě fyzikální veličiny, prostor a čas, jsou podložené pulsy hypotetického vesmírného generátoru. Všechny fyzikální veličiny předpokládám v podložení - vytvoření body, jejichž umístění sleduje časoprostorová geometrie.
Video - klasický popis souvislostí
ke Speciální teorii relativity, v sedmi modelových scénách.
Kružnice souměrného diagramu … nahrazuje vodorovnou stoupající přímku Minkowského diagramu
Perspektivní prostor … geometrický prostor, jenž vystihuje zrakové vnímání
Bod … informace 1 bitu o obsazení posice. Ta je buď obsazena nebo neobsazena
Posice … úložiště pro informaci 1 bitu. Je funkčně provázaná s dalšími posicemi. Například v 3D prostoru se šesti jinými okolními posicemi. Umožní bodu přesunout se do jedné z nich, na povel pulsu
Zdroj = časová základna … vytváří sled pulsů [PE]. Některé z nich, některým bodům, umožní přeskok do sousední posice. Foton, chápaný zde jako bod, přeskakuje při každém pulsu
Sled pulsů [PE] … Hodinový signál vytvářený Zdrojem
Silový puls [1 PF] … Změní dosavadní pohybový stav bodu. Například upraví jeho předchozí rychlost 0,1 posice/puls (1 posice/10 pulsů) na jinou
Pohybový puls [1 PL] … v něm bod opustil určitou posici a objevil se v sousední posici
Časový puls = puls (diskrétního) času [1 PT] … ten puls Zdroje, v němž uvažovaný bod neopouští svou posici
Diskrétní čas [PT] … součet pulsů, nevyužitých k přesunu bodu do sousední posice
Perspektivní čas [s2] … kvantita perspektivního času [s2] je rovna kvantitě diskrétního času [PT]. Tvor ji však vnímá stlačenou kvadratickým přepočtem
Čas (lineární) [s] … newtonovská či relativistická veličina, daná odmocninou ze součtu pulsů [PT], které bod nevyužil k přeskoku do jiné posice
Současnost … proces nabízející všem posicím, v uvažovaném diskrétním prostoru, přemístit body účinkem jednoho pulsu
Přítomnost … fyzikálně podmíněný pocit existence. Určuje ho perspektivní zpracování veličin časoprostoru. Příčinou pocitu přítomnosti je časový úsek při počátku souřadnic, protože je ze všech úseků nejdelší
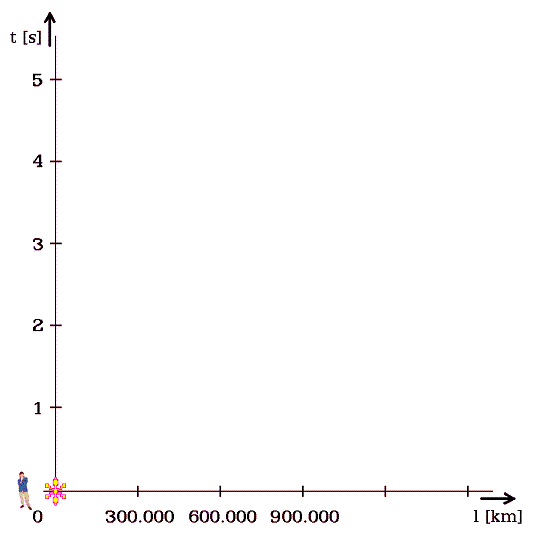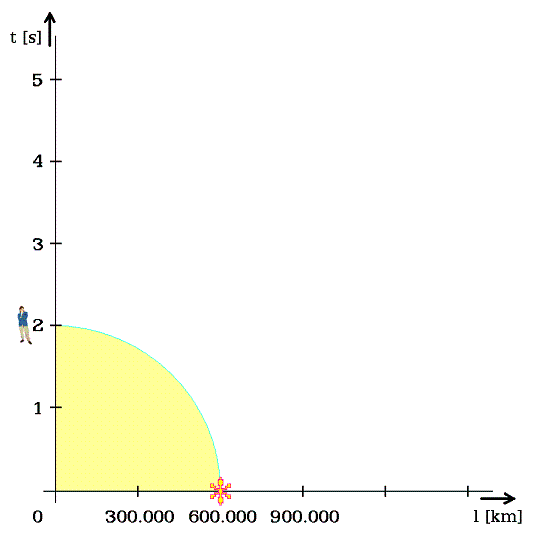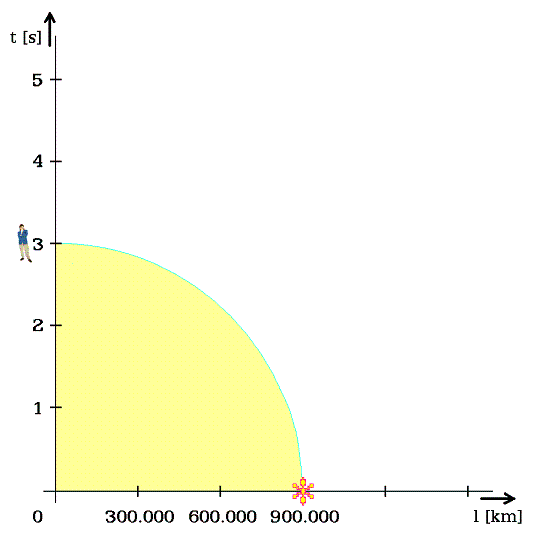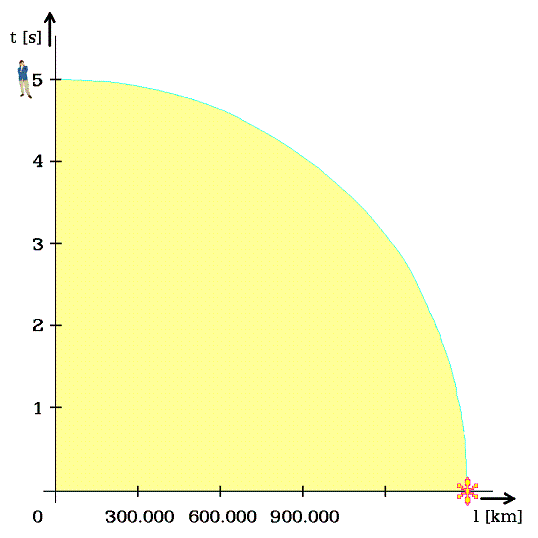
V Minkowského časoprostoru se nanáší na svislou osu čas (obr. 1). Kdežto nejrychlejší pohyb světla, asi 300.000 km/s, se nanáší jako šikmá polopřímka procházející bodem [300.000 km, 1 s]. Pozorovatel na Zemi, hvězdolet a foton vycházejí ze společného časoprostorového počátku. Vybarvený trojúhelník upozorňuje na dovolené rychlosti, omezené rychlostí pohybu světla. Zpomalený čas, platný na hvězdoletu, se z tohoto obrázku časoprostoru přímo nevyčte. Diagram odpovídá newtonovskému pojetí fyziky - nesleduje zpomalování času.
««« SLEDOVAT VŠECHNY OBRÁZKY I V LEVÉM SLOUPCI
V době začátku teorie relativity bylo potřebné zdůraznit omezené rychlosti pohybu. Hermann Minkowsky v diagramu zavádí fotonu šikmou čáru dráhy. Dovolené rychlosti pohybu ostatní hmoty pak náleží ploše mezi svislou osou a dráhou fotonu.
Jenže zmíněný obrázek nepředvádí rovnocennost času a prostoru.
Lorentzovu transformaci {1} lze převést do tvaru Pythagorovy věty {2}. Ta, stejně tak patří rovnici kružnice. Její zobrazení určí souměrný diagram. Ukáže rovnocennost času a dráhy v teorii relativity.
{1} Lorentzova transformace
t = t0/sqrt(1 – v2/c2)
{2} Pythagorova rovnice (v/c)2
+ (t0/t)2 = 1
v… proměnná rychlost sledovaného objektu [m/s]
t… proměnný relativistický čas [s]
t0… čas objektu bez pohybu [s]
c… rychlost světla [m/s]
Zpomalený růst času je provázaný s pohybem objektu. Tato funkce je popsaná výpočetně i pojmově: Lorentzovými přepočty i pojmem časoprostoru. Rychlému pohybu odpovídá zpomalený čas a naopak. Jejich propojenost zavedla pojem časoprostoru. Při našich nízkých rychlostech pohybů nezjistíme zpomalování času.
Minkowského diagram nyní nahradím tak, aby vynikla rovnocennost času a prostoru. Když nejrychlejší čas soustavy nanášíme na svislou osu, pak nejrychlejší pohyb zakreslím přímo na vodorovnou osu (obr. 2). Foton se v grafu pohybuje vodorovně, jeho čas zůstává nulový. Tento souměrný diagram sleduje relativistický čas.
V Minkowského diagramu stále stoupá přímka, jež značí současnost. Je rovnoběžná s vodorovnou délkovou osou. Kdežto v souměrném diagramu postupně roste kružnice, nahrazující onu stoupající přímku. Každému objektu, z obvodu kružnice, lze na svislé ose najít jeho vlastní čas (obr. 3).
Hvězdolet urazil dráhu 300.000 km a jeho vlastní čas je 2,8 s. Přitom na Zemi uplynul čas 3 sekundy a foton uletěl vzdálenost 900.000 km. Měření času v hvězdoletu a u postavy na svislé ose dává odlišné údaje. Přesto lze obhajovat pojem „přitom“, tedy současnost, jakožto vlastnost relativistické současnosti.Souměrný obrázek nabízí nadřazenou současnost tří objektů,
ačkoliv jejich časy jsou odlišné. Nacházejí se společně na obvodě
kružnice a tudíž mají stejnou časoprostorovou vzdálenost od
počátku. To lze, z nadřazeného pohledu, nazývat současností.
Hmotě v pohybu se čas zpomaluje, až se úplně zastaví fotonům. Fyzika nezná couvání času. Čas narůstá, nevracíme se v ději nazpět.
Jinak s pohybem objektu v prostoru. Minkowského diagram jej umožňuje ve směru doleva nebo doprava, vždy po vodorovné stoupající přímce.
Zde zavedený souměrný diagram jinak. Dodržuje rovnocennost času a pohybu, takže by neměl dovolit pohyby na vodorovné ose zprava doleva, směrem k počátku. Vždyť tím by objekt opustil obvod časoprostorové kružnice, jež stále rovnoměrně roste. Jenže my jsme zvyklí pohybovat se prostorem tam i zpět. Proto na vodorovnou osu patří absolutní hodnota překonané trasy; nezohlední směr pohybu. Ať vzdálenost od počátku vždy jen narůstá.
Známe-li pohyb jako obousměrný, lze přemítat, zda podobně i čas dovolí posunout objekt tam a zpět, směrem k počátku času. Na vodorovné ose nutno kreslit absolutní velikosti délky, pak i na svislé ose jsou jen absolutní velikosti, a jednou budou přece nalezeny souvislosti časového návratu do záznamu minulosti? Sůh buď, říkávali opatrní.
Poznámka: Užívám souměrný diagram - pohyb fotonů kreslený po vodorovné ose.
• Souměrný 2D časoprostor, zde zobrazovaný - vodorovnou osou je 1D geometrický prostor (obr. 3).
• Souměrný 3D časoprostor. Jemu přísluší dvojrozměrný geometrický prostor, kde by žili stínoví 2D tvoři. Rostoucí kružnici nahradí rostoucí koule (čtvrtkoule), se středem v počátku os. Svislá časová osa stojícího objektu se nezmění. Vodorovnou osu nahradí rovina. Foton v ní letí libovolným směrem. Jiné objekty, vzdalující se počátku, se zobrazí podle své rychlosti a směru letu na příslušném místě povrchu rostoucí čtvrtkoule.
• Souměrný 4D časoprostor. Diagramy pro náš 3D geometrický prostor se nekreslí. K zobrazení diskrétního časoprostoru bych použil diskrétní (bodové) čtyřrozměrné koule. Jednotlivé její koule by rostly, přibývající svým počtem ve čtvrtém směru 4D prostoru – jako náhrada kružnice souměrného 2D časoprostoru. Fotony by letěly v libovolném směru 3D objemu.
Poznámka: Soubor Zakřivení časoprostoru uvažuje o pohybu v 2D a 3D diskrétním časoprostoru.
V diskrétním prostoru popisuji přeskoky bodů, které vyjadřují hmotu. Odtud se informace přepočítávají do geometrie perspektivního prostoru, do lidského vnímání. Práce, které předkládám, neuvažují hmotu – ve všem sleduji jen lidské zážitky hmoty.
Euklidův prostor neužívám; body z diskrétního prostoru do něj přepočítat nelze. Naopak převod do zrakového perspektivního prostoru je racionální, s předpokladem dalších vyjasnění tohoto prostoru.
V diskrétním prostoru zavádím čas diskrétní - naskakující. Přibývá v pulsech, ale pozor - není to náš čas v sekundách. Pulsy nejsou naší jednotkou času, způsob přepočtu bude uveden v kapitole 10.2.
V diskrétním prostoru je všechna hmota podložena, každý její bod je umístěný v určité posici rastru. Bod hmoty posuzuji jako informaci 1 bitu o obsazení posice. Množství přepočítaných informací pak zásobuje vědomí tvora.
Body se přesunují do sousední posice vždy jen na povel. Hodinový signál hypotetického vesmírného taktovacího Zdroje opakuje své pulsy, a tím stále znovu nabízí přesun bodů. V jednom pulsu bod neuskuteční víc pohybů; vykoná buďto jediný nebo žádný přeskok z posice do sousední posice. Pulsace diskrétního světa takto podmiňuje jevy spojitého časoprostoru. Pokud bod přeskakuje v každém dalším pulsu Zdroje, pak letí rychlostí světla. Úhlopříčný pohyb bodů mezi dvěma posicemi ať není umožněn.
Kosmonaut letí těsně podsvětelnou rychlostí. Jeho hmota přeskakuje vždy do dalších sousedních posic opakovaně, než se konečně objeví jeden puls, nevyužitý pro přímočarý pohyb. Až tehdy se s bodem v posici nestane nic - anebo se pohne novým směrem, do kterékoliv ze sousedních posic. Například kosmonaut jen pomalu otáčí hlavou. K pohybu ze své vůle může využít jen těch pulsů, které koráb s jeho tělem k setrvačnému letu nevyužívá. Přitom však žádné zpoždění nezjišťuje. Ani svými smysly s myšlením, závislým na hmotě, ani hodinami.
Známý fyzikální případ letící částice prokazuje podobně. Ta vlétne obrovskou rychlostí do ovzduší Země. Srazí se s jádrem atomu v ovzduší, ve výšce desítek kilometrů. Následně vznikne nová částice - mion. Její životnost před rozpadem je krátká. Životnosti [s] by odpovídal dolet jen 600 metrů, a pak by se mion rozpadl na elektron a neutrina. Avšak ve skutečnosti letí mnoho kilometrů a i dopadne na povrch Země.
Tento jev je zdůvodněn zpomalením času v existenci mionu. Rozpadne se opožděně vůči mionům, které se vyskytují na Zemi.
Pulsní časoprostor nabízí podrobněji. Rozděluje trvání existence částice na okamžiky – pulsy – pohybové PL a časové PT. Mion v pulsu
Rotující kotouč v podsvětelné rychlosti zmenšuje svůj obvod - kdežto hmota uvnitř kotouče, vlivem své menší obvodové rychlosti, se tolik nezkracuje. To je problematický přístup speciální teorie relativity. Paradox spojitého prostoru – vnitřek kotouče by měl strpět zkrácení vnějších obvodových částí kotouče?
Okrajové body nijak nemizí z prostoru. Nezaviní drcení vnitřku kotouče, nýbrž okrajová hmota stárne pomaleji než pomalejší vnitřní hmota.
Naše Zeměkoule nechť má velmi malou rychlost setrvačného pohybu, když se přesunuje posicemi diskrétního prostoru. Proto mají pozemšťané možnost přesunu ve většině pulsů, které Zdroj vytváří. Procházíme životem vlastními pohyby rychleji než ti na podsvětelném kosmickém korábu; žádný dlouhotrvající translační pohyb nám nebrání, abychom využívali k zamýšleným pohybům nabídku skoro všech opakovaných pulsů Zdroje. Stárneme rychleji.
Na Zemi se hmota pohybuje pomalu; proto většina zdrojových pulsů, nabídnutých k pohybu, zůstává nevyužitá.
Na čas budou transformovány pouze ty pulsy vesmírného Zdroje, které se nevyužily na pohyb. Závislost převodu je nelineární (kap. 10.2.)
Hodiny nedokážou využít k drobným pohybům ruček všech pulsů, jež se jim nabízely jako nevyužité; těch je obrovské množství. Avšak počet tiknutí hodin je úměrný počtu těchto nevyužitých pulsů. A to při libovolné rychlosti letu hmotného objektu s hodinami. Dalšímu tiknutí přísluší jen ty pulsy, ve kterých hodiny s korábem nekonají společný translační pohyb. Pulsy PT, ve kterých hmota korábu v posicích vyčkává.
Počet tiknutí, úměrný počtu nevyužitých pulsů, ať souvisí s platností fyzikálních zákonů. Pokud by nebyly - veškeré pohyby v soustavě - podrobené jediné časové základně, společnému hodinovému kmitočtu, pak by se nedodržovaly zákony. Chemická reakce by proběhla jednou takovou rychlostí, jindy či jinde zase jinou rychlostí. Světlo by mělo rychlost tu větší, jindy bezdůvodně zase menší. Má se snad uznávat stálá rychlost světla bez zdůvodnění? Časová základna - Zdroj - je zde nutností. Její existenci nasvědčuje relativistické zpomalování času při pohybu, které dosud nebývá příčinně zdůvodňováno. Zde navrženým postupům nenacházím rozpor vůči Lorentzovým transformacím.
Naše měření času využívá pohybu. Ať kmity kyvadla nebo nepokoje, nebo kmitání částice hmoty.
K tiknutí, k vnitřnímu pohybu mechanismu, se využívají pouze některé z pulsů PT, které letící celek k translaci nevyužil. Určitý počet pulsů, jež pohybově využily právě hodiny, určuje zvolená jednotka. Například ať jednu sekundu tvoří 2·1043 nevyužitých pulsů - na základě Planckova času 5,39121·10-44 s.
Nepřesné hodiny reagují např. na každý 1044. (desátý na čtyřicátou čtvrtou) puls. Jiné, pracující vysokým kmitočtem, tiknou při každém 1040. (desátém na čtyřicátou) pulsu. Vždy je lze cejchovat tak, aby dávaly údaj úměrný časové jednotce, tedy jistému počtu nevyužitých pulsů.
Diskrétní „čas“ hodnotím následovně. Příležitost k pohybu bodu nebyla využitá, proto se hmota tímto pulsem nezměnila. Odehrával se snad nějaký fyzikální proces na svislé ose Minkowského nebo souměrného diagramu (obr. 3)? Ne. Časová osa vystihuje pouze předstih jednoho děje (přesunu bodů hmoty) před jiným - v závislosti na různých rychlostech pohybu. Lze pochybovat o fyzikální podstatě času.
To bylo hodnocení z hlediska diskrétních veličin; kdežto spojitým veličinám jinak. Čas je spojitému prostoru důležitý, pomáhá fyzikálním výpočtům.
Dále zobrazím užití pulsů na pohyb nebo na čas; pro tři koráby (obr. 4). Každý koráb má jinou rychlost pohybu v bodovém prostoru a určuje ji jen setrvačnost. Na horní ose n [puls] se prodlužuje řada pulsů, která znázorňuje trvalý chod jejich Zdroje. Dolní obrázek užívá pulsy dvěma způsoby:
׀ modrá barva označuje nevyužité pulsy PT,
׀ zelené pulsy PL
značí přeskok bodu do sousední posice.
▪ Spodní koráb má skoro rychlost světla; zastaví se na trvání 1 pulsu až po mnoha pohybových pulsech.
▪ Prostřední koráb využívá každý druhý puls k pohybu.
▪ Horní koráb neodstartoval; má nejrychlejší čas. Jeho hmota by
korodovala nejrychleji, protože ji při okysličování nezdržují
translační pohyby korábu posicemi diskrétního prostoru.
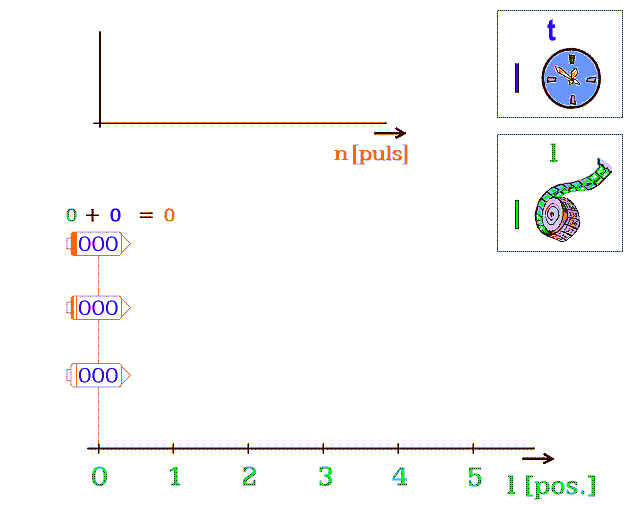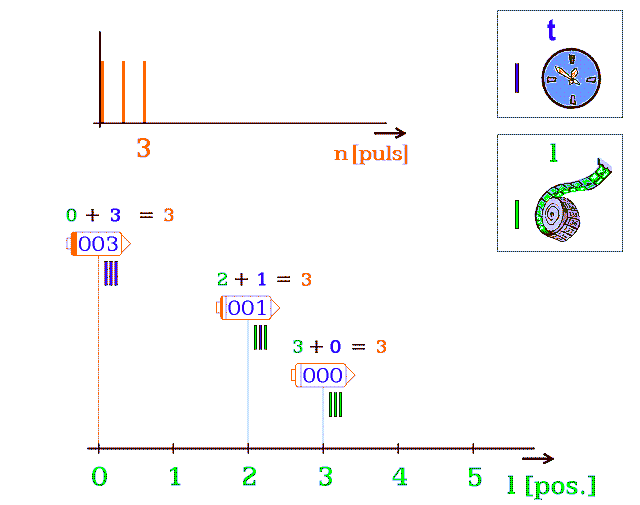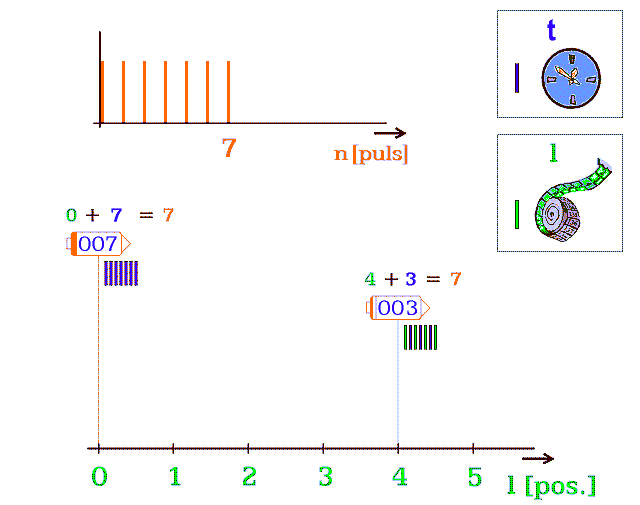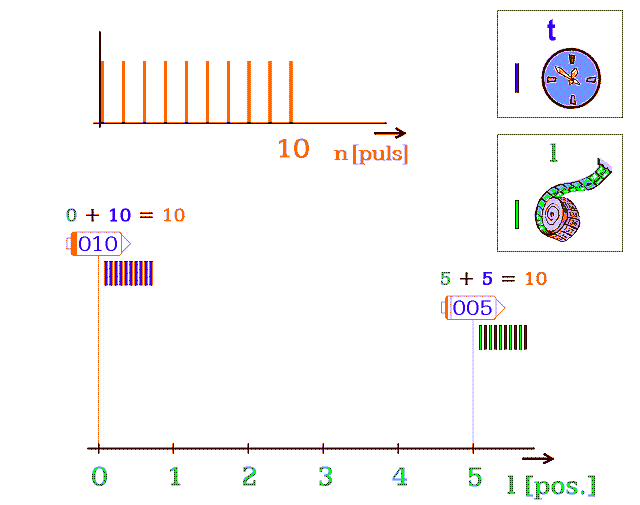
Obr. 4.b Tři vesmírné koráby v různých rychlostech
pohybu. Čísla v korábech značí jejich diskrétní „čas“ -
počet pulsů nevyužitých k translaci. Součet dvou čísel,
nad korábem, počítá dosud proběhlé pulsy. Diskrétní „čas“
v pulsech není časem v sekundách (viz 10. kapitola)
Pohyb bodu v posicích bodového prostoru má buďto rychlost světla, nebo se pohyb neuskuteční. To platí i pro naši pomalou hmotu na Zemi. Přeskok z jedné posice do sousední má jedinou rychlost pohybu: 1 posice/1 puls. Malá spojitá rychlost pohybu je pak daná nepatrným využitím zdrojových pulsů. Prostřídá se nám malý počet pohybových pulsů PL a velký počet časových pulsů PT - těch nevyužitých k pohybu.
Bod hmoty diskrétního prostoru jsem již výše hodnotil jako informaci 1 bitu o obsazení posice.
Když měníme rozložení hmoty, využíváme přitom času?
Naopak. Čas je podložený nevyužitými okamžiky. Na hmotě se vůbec neuplatnily. Nestárneme v čase, nýbrž právě v těch pulsech, které jsou využité pro pohyb – to z hlediska diskrétní nauky. Například pro chemické reakce v buňkách těla.
O čase obvykle soudíme, že je podmínkou změn, tedy i pohybu.
Jenže zvolený diskrétní přístup nabízí opačný názor. Právě pro bod
v pohybu čas není. Když hmota využívá časoprostorových pulsů
k pohybu, pak jí čas nepřibývá. U fotonu se to projeví
naprosto. Čas je pojmem newtonovské a relativistické fyziky.
Diskrétní základ Vesmíru uvažuje o jeho podstatě.
Hmota se vlivem nevyužitého pulsu vůbec nezměnila. Nečinnost však není nicotností; nevyužitý puls přece něco značí. Konání v podsvětelném objektu se opožďuje oproti pomalejšímu objektu. Rychlý stárne pomaleji.
V souměrném diagramu vznikla čtvrtkružnice o stále rostoucím průměru (obr. 2). Tomuto ději hledám příčinu. Rostoucí kružnici nezdůvodním pojmem časoprostoru, protože toto spojení času a prostoru (časoprostor) fyzika tradičně vysvětluje jako množinu událostí a jako jistý druh prostoru [1][2][3][4][5][6].
Růst časoprostorové kružnice podmiňuji Zdrojem, který ovládá pohyb v prostoru. Fyzikální podstata času se mi, zde zavedenými postupy, jeví být bezobsažným pojmem (kap. 7). Ovšem v denním životě bývá potřebný. Chod hypotetického Zdroje podkládá všechny fyzikální veličiny. Zdroj umožňuje bodům hmoty jejich pohyb; podle stanovených zásad, jež předpokládám vestavěné do prostorových posic.
Pulsní Zdroj zdůvodní současnost v uvažovaném prostoru, neboť zdrojové pulsy jsou mu vytvářené naráz. Ovšem je možné, že každá sluneční soustava má svůj časoprostor - svůj pulsní zdroj, jak naznačuje [7]. Konstrukce Vesmíru je promyšlená, a pak se to jeví být přijatelné.
Zdroj a posice umožňují vnímat zážitky a snad jsou sestavené z hmoty, kterou svými smysly nevnímáme. Podobně jako divák televize, vzdálený od ní, nezjišťuje hmatem její skutečnost; pouze vnímá výsledky její činnosti. Stejně tak člověk nevnímá posice diskrétního prostoru.
Nejvyšší možný kmitočet elektromagnetického záření je podmíněn pulsací. Obyvatelé časoprostoru nemají možnost posoudit rovnoměrnost - stálost kmitočtu použité pulsace. Hlubší posouzení Zdroje zůstává neupřesněné.
Zdroj, zde navržený, stejně tak zdůvodní stoupající přímku Minkowského diagramu.
V diskrétním souměrném časoprostoru umísťuji tři objekty: postavu, koráb a foton (obr. 5). Všechny jsou v časoprostorové vzdálenosti 2·1050 pulsů od počátku. Šikmá modrá úsečka se vzdaluje počátku; prodlužuje se. Její délka roste následkem přibývajícího počtu zdrojových pulsů, který soustavu vzdaluje od časoprostorového počátku. V diskrétním prostoru šikmá úsečka zaměňuje čtvrtkružnici ze spojitého souměrného diagramu (obr. 2).
z1 … vzdálenost objektů od počátku
[puls]
zt … nevyužité pulsy [PT]
zl … pulsy využité k pohybu [PL]
- stojící postava na svislé ose je prožije bez pohybu. Na časové
ose je posunuta do bodu 2·1050 PT,
- foton se dostane do vzdálenosti 2·1050 PL,
- kosmický koráb k pohybu využije polovinu pulsů a dostane se do vzdálenosti 1·1050 PL. Pulsy pohybové střídal stejným počtem 1·1050 pulsů bez pohybu, PT.Nebo je možné i jakkoliv jinak rozdělit z1 = 2·1050 pulsů: například 1.000 pulsů na pohyb (PL) a (2·1050 – 1.000) pulsů je nevyužitých (PT).
Pro určení počtu pulsů, které vytvoří délku 1 metr nebo čas 1 sekundu, lze vycházet z Planckových konstant. Nabízí se Planckův čas přibližně 5,39·10-44 sekund jako nejmenší velikost času, kterou vytvoří jeden nevyužitý puls Zdroje. Jednu sekundu by tak tvořilo 1/(5,39121·10-44) = 1,85487·10+43 pulsů.
Planckova délka přibližně 1,62·10-35 m je nejmenším známým dílem délky. Po převrácení sdělí počet pulsů, tedy počet přeskoků na trase 1 metr u fotonu ve vakuu: 1/(1,61624·10-35) = 6,18719·10+34 pulsů.
Euklidův prostor nabízí, pro zdůvodnění smyslového vnímání, jisté
rozložení hmoty ve Vesmíru. Velikost zrakového vjemu se v něm
přesvědčivě odvozuje ze zorného úhlu.
Jenže tento prostor zpochybňují iracionality. V geometrii
známe úsečky jediného druhu; liší se pouze délkou. Avšak
matematické vyjádření délky je dvojí; buďto racionální nebo
iracionální.
Namítám nevhodnost Euklidova prostoru pro vyjádření skutečností našeho světa. Vždyť exaktní matematické vyjádření délek úseček někdy chybí - tím se liší od jednoznačného vyjádření geometrického.
Dále Euklidův prostor neumožňuje převzít údaje z diskrétního prostoru. Hodnocení přeskoků mezi sousedními posicemi v úhlopříčném směru se u obou prostorů liší. Perspektivní prostor nemá tento problém.
Náš smyslový svět není přímo tvořen diskrétními body. Ty totiž nevytvoří ideální kružnici, kterou známe z denního života a z Euklidova prostoru.
Odedávna se vyskytovali filosofové zdůrazňující, že na hmotu usuzujeme ze svého smyslového vnímání. Kdežto, co za vjemy je, o tom lze spekulovat - avšak nezlehčujeme svým dosavadním výběrem prostorů význam matematiky? V Euklidově prostoru uvažujeme tu a tam vzdálenosti racionální, pak zase iracionální - některé vzdálenosti lze spočítat, jiné výsledek nedají. Tím je zvolený Euklidův prostor stěží obhajitelný k vysvětlení našeho světa! Ačkoliv různé souvislosti tohoto prostoru jsou zpracované do mimořádné hloubky, ve prospěch lidského poznání.
Údaje z prostoru diskrétního převádím
rovnou do perspektivního. Do vnímání našich smyslů - zraku a
sluchu (obr. 6). Vynechávám Euklidův lineární prostor.
Souřadnice, rozložené na osách, umocním na druhou. Tento prostor
neobsahuje nevypočítatelné vzdálenosti; je nepochybně
matematizovatelný. Kterýkoliv bod prostoru diskrétního lze najít
v perspektivním. Bude mít stejnou vzdálenost od počátku, a i
stejné kartézské souřadnice.

Obr. 6. Zdroj pulsů určuje pohyb ve spojitém perspektivním časoprostoru
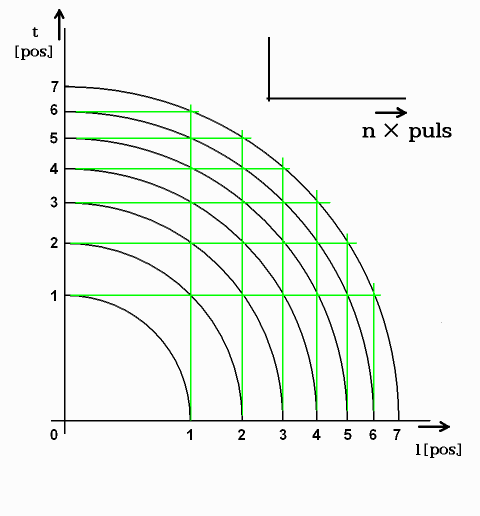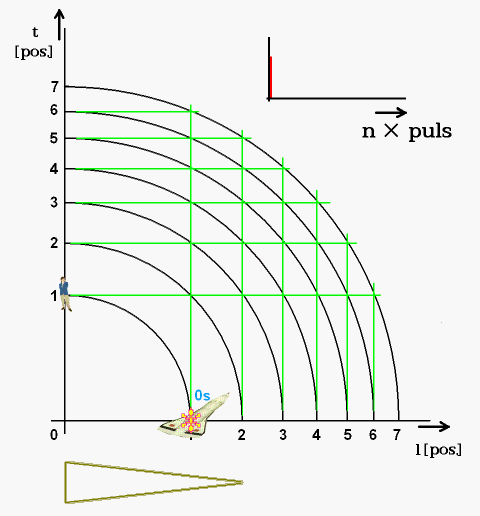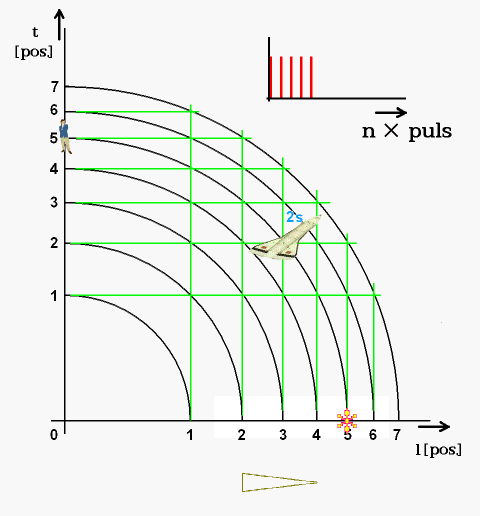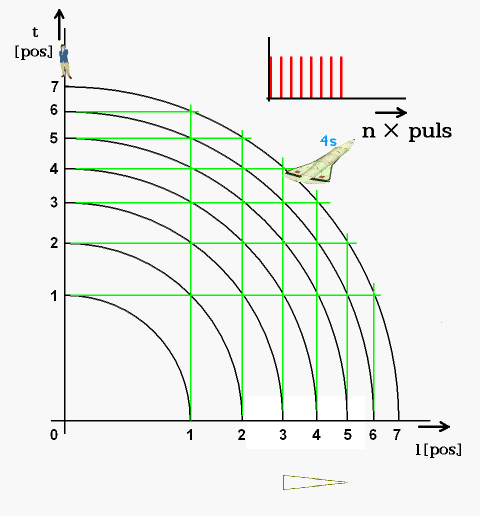
Obr. 7. Síť zdůrazňuje souvislost perspektivního prostoru s diskrétním
Obr. 8. Spojité perspektivní vnímání. (10 pulsů ať zde tvoří 1 s)
tEu… lineární čas [s]
tq… perspektivní (kvadratický) čas [s2]
Převod z diskrétního do spojitého prostoru řeším perspektivně stlačenými souřadnicemi délkovými, a stejně tak i časovými. Vzniká perspektivně stlačený časoprostor.
V nelineárním časoprostoru jsou děje, vnímané tvorem v blízkosti počátku souřadnic, posílené největší délkou úseku 0-1, kdežto ostatní úseky jsou stále kratší. Neustálý životní vjem časové přítomnosti lze vysvětlovat časovou perspektivou - obdobně, jak ji známe ze zrakového vnímání. Pak lineární čas nemá být základní životní (světovou) skutečností.
Hodiny sdělují lineární čas. Lze hledat podobnost s opakovaným prvním krokem při chůzi, jenž vnucuje životní pocit lineárního Euklidova prostoru, ačkoliv zrakový vjem délky je jiný. V souladu s konečnými racionálními výpočty. Pak i představa lineárního času je šálivě připomínána prvním krokem, jejž ručka hodin učiní vždy pro stejný časový úsek.
Obr. 9. Diskrétní stav po 20 pulsech
Postava v těchto 20 zdrojových pulsech čeká, prožije 2 s2 (perspektivního času). To je √2 s lineárního času, který běžně používáme, ve který věříme. Hvězdolet využije 20 pulsů smíšeně. Jeho hodiny naměří 1 sekundu a od počátku se vzdálí 1·300.000 km, na kvadratické ose 300.0002 km2.
Obr. 10. Spojité perspektivní vnímání s vyznačením rastru. (10 pulsů ať zde tvoří 1 s)
Ve výpočtu E = m·c2 se vyskytuje kvadrát rychlosti. Transformací do perspektivního prostoru nutno změnit jak délku - perspektivně, a stejně tak i čas. Pak v rovnici bude rychlost zavedena v první mocnině.
Perspektivní (kvadratický) prostor neuvažuji pro výpočetní
využití. Nýbrž je nabídkou alternativního názoru na konstrukci
Vesmíru, ve kterém žijeme. Výpočetní užití by mohlo být nalezeno
spíš v diskrétním prostoru, jímž je perspektiva podložena.
Spojité údaje, předkládané našimi smysly, vyhodnocujeme svým
vědomím. Vnímáme zážitky hmoty, perspektivně rozmístěné.
Každé jedno vědomí, opatřené zážitky hmoty, může vnímat svůj
samostatný vesmír. To dovoluje existenci mnoha dalších, například
vícerozměrných vesmírů, které se prostorově neovlivňují. (Viz blokové
schéma člověka, kap. 0.2.1. Nezávislé vesmíry)
Námitkou proti diskrétnímu prostoru, jako působišti pro částice hmoty, bývá Heisenbergův princip neurčitosti. K čemu hledat naprosto přesné umístění částic, když se částice přemísťují náhodně?
Zdůvodnění se nabízí: Například částice ať je složená z obrovského počtu hmotných bodů. Má-li existovat - např. elektron, pak se seskupení těchto bodů nesmí rozpadnout. Při přeskocích body respektují svůj celek. Kdežto tento celek nepřeskakuje do předepsaných posic. Částice, jako celek, sleduje neurčitost.
Taková upřesnění lze vyhledávat stále dál; zde autor - laik, se pokouší jen o představu nejstručnějších základů.
Vysvětlení relativistické hmotnosti zkouším spojovat se
zdrojovými pulsy. Její nárůst je nabízen zpomalováním času.
Uvažuji koráb letící obrovskou rychlosti, jenž je dál urychlován reaktivním pohonem. Velkou rychlost určil dlouhý sled pohybových pulsů PL, a malý počet časových pulsů PT, jimiž se PL prokládají. Sledem PL se další zrychlující účinek spuštěného raketového motoru odkládá na později, na pulsy PT. Podsvětelný koráb bude postrčen motorem na vyšší okamžitou rychlost až tehdy, když se vyskytne nevyužitý puls PT. Korábu se tím změní na PL. Hořící palivo reaktivního pohonu, po mnoho pulsů PL, podléhá pouze translačnímu pohybu a nemění se. Stejně tak celý koráb. Během pohybových pulsů PL nelze koráb urychlovat, což se obvykle posuzuje jako zvětšení hmotnosti.
Vyhodnotím-li situaci pozemským časem, pak se počet molekul spotřebovaného paliva, za jednotku pozemského času, nutně snížil. Zpomalený korábový čas mám za bezprostřední příčinu zhoršeného urychlování korábu. Zde usuzuji jinak, než je tomu ve speciální teorii relativity.
Když nález zkusím přenést z diskrétního prostoru do spojitého, pak nárůst relativistické hmotnosti je výhradně projevem zpomaleného času. Následek - zdánlivý růst hmotnosti korábu, v podsvětelné rychlosti, by nezvyšoval požadavky na mechanickou pevnost korábu.
Dotýká se i souvislostí v urychlovači částic. Ačkoliv „hmotnost se při pohybu zvětšuje“ a tudíž pak částice svazku v urychlovači potřebují větší energii k urychlení, přesto vzájemná přitažlivost souběžně letících částic ve svazku paprsků údajně není ovlivněna. Diskrétní podstata relativistické hmotnosti - nedostatek nevyužitých (časových) pulsů, může být vysvětlením ztíženého urychlování. A tento nedostatek pochopitelně nemá vliv na vzájemnou přitažlivost částic, v těchto mých nejjednodušších představách.
Zdrojovým pulsům jsem popsal jejich pohybové uplatnění. Dále na bod hmoty působí gravitace. V náročné obecné teorii relativity najdu i jeden lehce srozumitelný závěr - zpomalování času je způsobeno také gravitací. Dalším způsobem působení pulsů ať je, kromě pohybu, i síla.
Bod, vzdalující se planetě setrvačností, obsadí další posici. Ta jej, kvůli gravitaci, následně uvolní až o něco později, až po více pulsech – než by bylo v prostředí bez gravitace. Případně, v opačném směru, bude přitažlivostí urychlen či se změní směr přeskoků.
Jeden z pulsů byl využitý na chvilkové zadržení letícího bodu v posici, ačkoliv dle své setrvačnosti ji měl již opustit. Bod v posici setrval, a přesto se mu čas (PT) nezapočítá. Silový puls (PF) nedovolil přeskočit, ačkoliv v situaci bez gravitace by tomu bylo jinak.
Bod je informací a proto mu nepřísluší hmotné - silové působení. Původcem gravitace odhaduji funkci, zabudovanou do posic diskrétního prostoru. Posice zajišťují setrvačnost v pohybu bodů a i jejich zrychlení, které způsobí síla.
Maxwellovy rovnice určují stálou
rychlost světla. Posoudím, jak v diskrétním časoprostoru.
• Objekt zůstává v totožné posici během uvažovaného pulsu; je bez pohybu. Tehdy se fotony, směřující k němu či od něho, pohybují vůči němu stálou rychlostí. Situace vyhovuje Maxwellově podmínce stálé rychlosti světla.
• Naopak když objekt přeskočí určitým směrem, tehdy se mu nevzdalují fotony, jež letí v tomtéž směru. Přeskočí shodně s objektem. Zde spekuluji o existenci bodu. Jak je bod definovaný v pulsu přeskoku? Zřejmě pouze probíhá proces obsazení sousední posice. Proces může nebo nemusí být úspěšný, tudíž vzniká pochybnost o posici, ve které se měl objekt (pozorovatel) nacházet. V původní nebo v nové posici?
Konstanta „c“ sice není dodržena, ale v pohybovém pulsu snad hmota neexistuje. Možná bod obsadí sousední posici, možná ji neobsadí, pokud ta už obsazená je. Maxwellova konstantní rychlost světla se nabízí jen pulsům, ve kterých pozorovatel z posice nevyskočí ani do ní nedoskočí. Kdy má puls časový.
Podle Maxwella je „c“ ve spojitém prostoru konstantní. Ale v diskrétním prostoru může být tento poznatek zpřesňovaný různými způsoby. *)
*) Spekulace jinde: 7. Světová virtuální realita vysvětlená rychlostí světla - Nepohybuje se v posicích hmota pozorovatele, nýbrž se posunují vnímané zážitky hmoty sluneční soustavy okolo něho, okolo pozorovatele.
V teorii relativity se neodliší absolutní pohyb nebo klid, protože základem je rychlost světla. Pokud snad klid či pohyb nejsou ve speciální teorii relativity jednoznačně definované, pak tato problematika může mít svůj vývoj ještě před sebou. Také s ohledem na omezené chápání „fyzikální veličiny“ času; kdežto možnost promyšlenějšího posuzování diskrétních pulsů předpokládá další souvislosti.
Ve světě, který posuzujeme jako Euklidův, je zdůvodňování konstantní rychlosti světla obtížné. Neřeší se vůbec, je postulátem. Jinak v perspektivně stlačeném světě, kde pozorovatelovo sídlo zraku je zcela objektivně středem prostoru s nelineárně rozloženou hmotou. Toto prostorové zavedení pomáhá názoru, že světlo se šíří od středového pozorovatele na všechny strany stálou rychlostí. Dominantní středová poloha pozorovatele vyhoví - lépe než rovnoměrný Euklidův prostor - požadavku všesměrové stálé rychlosti světla. Může snad další hledání naznačit soulad objektivních měření rychlosti světla vůči představě pozorovatele v perspektivním prostoru?
Není snadné srovnávat, jak na sebe navazuje několik perspektivních prostorů několika středových pozorovatelů.
Nabízím jen nejjednodušší návrhy, které motivuji speciální teorií relativity. Předpokládám, že tato práce ponouká k hlubšímu vysvětlování fyzikálních otázek, založených na mechanických modelech.
Vesmír připodobňuji technickému výrobku.
(Viz též kap. 2. Možný přínos zde představeného mechanického modelu)